Descartes et les Mathématiques

Épreuve pratique de terminale S supprimée

Sujets 2009 de géométrie plane avec GeoGebra

L'épreuve pratique de géométrie avec GeoGebra. Feuille de travail dynamique.

Sommaire

24. Étude d'une courbe de Bézier
65. Distance minimale d'un point à une courbe
69. Intersection de tangentes
Alignement avec un point et son transformé dans une similitude
76. Recherche d'un point fixe
81. Aire variable d'un triangle
83. Optimisation en géométrie plane
91. Propriétés de la courbe représentative d'une fonction
128. Étude de la courbe représentative d'une fonction
131. Étude d'une figure du plan

Version classique non interactive

Avec GéoPlan
Corrigé 2009

Épreuve pratique
Corrigé 2008

Épreuve pratique
Corrigé 2007

L'espace en
2007 et 2008

Cette année 2009, presque plus de géométrie plane ; seulement deux sujets sur les similitudes
(tous les deux déjà traité …avec GéoPlan) : une question de cours simplifiée et un exercice de spécialité.
Les autres sujets concernent uniquement l'étude de fonctions par un logiciel de géométrie dynamique.

24. Étude d'une courbe de Bézier

Énoncé

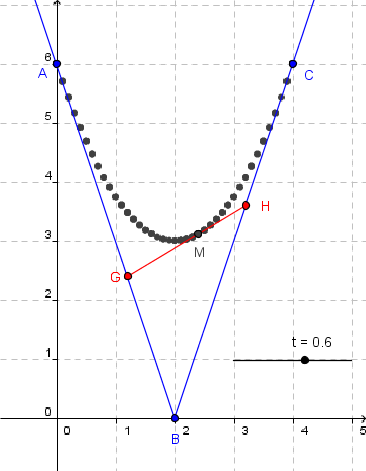
Dans le plan rapporté à un repère orthonormal (O, , ), on considère les points A de coordonnées (0 ; 6), B de coordonnées (2 ; 0) et C de coordonnées (4 ; 6).
Soit t un réel de l'intervalle [0 ; 1]. On définit les points :
  • G barycentre du système de points pondérés {(A; 1 − t) ; (B; t)} ;
  • H barycentre du système de points pondérés {(B; 1 − t) ; (C; t)} ;
  • M barycentre du système de points pondérés {(G; 1 − t) ; (H; t)}.

Le but de l'exercice est d'étudier le lieu des points M quand t décrit l'intervalle [0 ; 1], et la position de cet ensemble par rapport aux droites (AB) et (BC).

Partie A

1. Réaliser la figure avec un logiciel de géométrie dynamique.
    Tracer les droites (AB) et (BC), puis faire apparaître le lieu décrit par le point M lorsque t varie.
    Appeler l'examinateur pour lui montrer le lieu du point M.
2. Quelle semble être la position des droites (AB) et (BC) par rapport au lieu obtenu ?
3. Sur quelle courbe semble se déplacer le point M ?
    Appeler l'examinateur pour annoncer les conjectures et décrire la démarche.

Partie B

4. Déterminer en fonction de t les coordonnées des points G, H et M.
5. Valider ou invalider la conjecture émise à la question 3.
    Donner l'expression analytique du lieu du point M.

Production demandée

  • Visualisation du lieu du point M.
  • Énoncé des conjectures : courbe décrite par le point M et position des droites (AB) et (BC) par rapport à cette courbe.
  • Réponses pour les questions 4. et 5.

Technique GeoGebra

Le barycentre G des deux points pondérés (A, α) et (B, β),
tels que α + β ≠ 0, s'écrit : G = (α A + β B)/(α + β).

Pour garder la trace du point M, cocher l'option « activer le mode trace » dans le menu contextuel de M et déplacer le curseur de t.

Indications

2. Les droites semblent tangentes à la courbe.

3. Le point M se déplace sur la parabole d'équation
f(x) = (x − 2)² + 3.

Avec GeoGebra, cocher la case de f pour afficher le graphe.

4. D'après la fonction vectorielle de Leibniz = (1 − t) + t . Soit G(2t ; 6(1 − t)).
De même = (1 − t) + t . Soit H(2(1 + t) ; 6 t).
Enfin = (1 − t) + t . Soit M(4t ; 12t² − 12t + 6).

5. On a donc t = x/4 et y = x² − 3x + 6, équation de la parabole conjecturée à la question 3.

f’(x) = x − 3.  f’(0) = −3 et  f’(4) = 3. Les droites (AB) et (BC) sont respectivement tangentes en A et C à la parabole.

Figure dans GeoGebraTube : Courbe de Bézier - Épreuve pratique 2009

65. Distance minimale d'un point à une courbe

Énoncé

Dans un repère orthonormal d'origine O, on considère la courbe C représentative de la fonction logarithme népérien.
On s'intéresse à la distance OM lorsque M parcourt C. Le but de l'exercice est de préciser si cette distance peut être rendue minimale et de caractériser le ou les point(s) M, s'il en existe, situé(s) sur C et rendant cette distance minimale.

Partie A

1. À l'aide d'un logiciel de géométrie dynamique, faire une figure permettant d'explorer cette situation.

2. Cette distance semble-t-elle minimale pour un (ou plusieurs) point(s) particulier(s) de C ? Si oui donner une valeur approchée à 10^{– 2} près de cette plus petite distance et de l'abscisse de ce(s) point(s).
Appeler le professeur pour une vérification de la figure construite et des conjectures émises.

3. Tracer la droite (OM) ainsi que la tangente en M à la courbe C. Que semble-t-il se passer
lorsque M est positionné sur la courbe C de sorte que la distance OM soit minimale ?
Appeler le professeur pour une vérification de la conjecture.

Partie B

4. Quelle relation doit vérifier l'abscisse x₀ d'un point M₀ en lequel la distance OM est minimale ?
Appeler le professeur pour lui présenter la méthode envisagée et une vérification de la relation éventuellement obtenue.

5. Prouver la conjecture élaborée dans la question 3.

Production demandée

    – Les différentes étapes des stratégies prévues pour répondre aux questions 4. et 5.
    – La mise en forme de l'une de ces étapes.

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Indications

2. x₀ ≈ 0,43.

3. La droite OM₀ semble perpendiculaire à la tangente (d).

4. Le produit des coefficients directeurs, e^x / x pour OM et e^x pour (d), est égal à −1, d'où l'équation e^2x = − x et la solution approchée

5. Pour cette démonstration, basée sur la convexité de la courbe exponentielle, s'inspirer du même exercice proposé en 2008.

Télécharger la figure GeoGebra distance_point-courbe.ggb

69. Intersection de tangentes

Énoncé

On considère les fonctions f et g définies sur R par :
f (x) = (e^1+x + e^1−x)/2 et g(x) = (e^1+x − e^1−x)/2.
On note C_f la courbe représentative de f et C_g la courbe représentative de g.

Pour tout réel a, on note :
  – A le point de C_f d'abscisse a et T_A la tangente à C_f au point A,
  – B le point de C_g d'abscisse a et T_B la tangente à C_g au point B,
  – M(x_M ; y_M) le point d'intersection des tangentes T_A et T_B.

On souhaite étudier le lieu géométrique L du point M lorsque a varie dans R.

Partie A

1. À l'aide d'un logiciel de géométrie dynamique :
(a) Construire les courbes C_f et C_g ainsi que les tangentes T_A et T_B.
(b) Construire le point M.
(c) En observant la situation obtenue avec plusieurs valeurs de a, dire quelle relation semble exister entre les réels a et x_M.

2. Tracer le lieu L du point M. Ce point semble appartenir à la courbe représentative E d'une fonction connue, quelle est cette fonction ? Comment peut-on vérifier cette conjecture ?

Partie B

3. Démontrer que L fait effectivement partie de E. Que dire de plus ?

Production demandée

• Courbes demandées aux questions 1 et 2.
• Réponse à la question 3.

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Indications

1. Pour l'étude du lieu, on se limite avec GeoGebra à l'intervalle [−5 ; 5].

En déplaçant a, on trouve les valeurs suivantes :

(c) En observant le tableau de valeurs de a, on trouve la relation x_M = a + 1.

2. Le point M semble appartenir à la courbe représentative E de la fonction exponentielle.

On peut vérifier cette conjecture en traçant avec GeoGebra la fonction e(x) = e^x.

3. Un calcul de dérivée permet de trouver que f’(x) = g(x) et que g’(x) = f(x), d'où les coefficients directeurs g(a) et f(a) des tangentes T_A et T_B.

La tangente T_A a pour équation y − f(a) = f’(a)(x − a) d'où : y − f(a) = g(a)(x − a).
De même, T_B a pour équation y − g (a) = f(a)(x − a).

Résoudre ce système en éliminant y entre ces deux équations. En simplifiant par f(a) − g(a) on trouve x = a + 1.
Puis en remplaçant cette valeur dans une des équations on a y = f(a) + g(a) = e^a.

On peut dire en plus que L = E car tous les points de E sont atteints : en effet quel que soit M dans E d'abscisse x_M, M est le point d'intersection des tangentes aux points A et B d'abscisse x_M − 1.

Télécharger la figure GeoGebra intersection_tangentes.ggb

Alignement avec un point et son transformé dans une similitude

Un point A fixe et un point M variable sont placés sur un cercle (c₁).
Une similitude de centre A transforme le cercle (c₁) en un cercle (c₂) et le point M en un point M’.
Les cercles (c₁) et (c₂) ont comme deuxième point d'intersection B.
Montrer que les points M, B et M’ sont alignés.

Figure GeoGebra

La similitude est la composée d'une rotation de centre A suivie d'une homothétie de centre A et de rapport r₂/r₁. M a pour image M₁ par la rotation, M₁a pour image M’ par l'homothétie.

Démonstration

Calculer l'angle (, ) = (, ) + (, ) [mod π].

Les angles inscrits sont égaux à la moitié de l'angle au centre :
(, ) = (, ) [mod π],
(, ) = (, ) [mod π].

Dans la similitude A est point fixe, O₁ a pour image O₂, M a pour image M’, par conservation des angles on a (, ) = (, ) [mod π].
D'où – (, ) = (, ) et (, ) = 0 [mod π] ce qui prouve l'alignement.

Figure interactive dans GeoGebraTube : alignement dans une similitude

Démonstration avec les angles inscrits, voir : angles inscrits en troisième,

cas particulier de cercles de même rayon, voir : rotation en seconde.

76. Recherche d'un point fixe

Situation
Dans le plan orienté, on considère un triangle et un cercle.
Il s'agit d'étudier la position de la droite (MM’), où M est un point du cercle et M’ son image par une certaine similitude.

Énoncé

Dans le plan complexe orienté, on considère un triangle OO’A de sens direct, rectangle en O. On considère M un point du cercle C de centre O et passant par A. On désigne par S la similitude directe de centre A qui transforme O en O’ et on désigne par M’ le point image de M par la similitude S. On cherche à prouver que la droite (MM’) passe par un point fixe.

1. À l'aide d'un logiciel de géométrie plane, construire la figure associée à la situation décrite ci-dessus.

2. Construire l'image C’ du cercle C par la similitude S. Caractériser cet ensemble C’.

3. Quelle conjecture peut-on émettre pour la droite (MM’) lorsque M décrit le cercle C ?
Appeler l'examinateur pour une vérification de la construction faite.
On appelle A et B les points d'intersection de C et C’.

4. On pose S(B) = B’. Quelle propriété relative est vérifiée par les triangles ABB’ et AOO’ ?
Justifier.

5. Positionner le point M afin que le point B soit entre les points M et M’.

6. Donner des arguments mathématiques permettant de prouver que les points M, B et M’ sont alignés.

Production demandée

• La figure réalisée avec le logiciel de géométrie dynamique.
• La caractérisation de l'ensemble C’.
• La justification de la propriété de la question 4.
• La justification de la conjecture de la question 3. seulement dans le cas où le point B est entre les points M et M’.

Figure GeoGebra

La " similitude " est la composée d'une rotation de centre A suivie d'une homothétie de centre A et de rapport r₂/r₁. M a pour image M₁ par la rotation, M₁a pour image M’ par l'homothétie.

Indications

2. A est le point fixe de la similitude. L'image du cercle C de centre O et passant par A est le cercle C’ de centre O’ et passant par A.

3. Les points M, B et M’ sont alignés.

4. Les triangles ABB’ et AOO’ sont semblables par définition de la similitude. Comme AB est le double de AO, AB est le double AO’, [AB’] est un diamètre de (C’) et (BB’), perpendiculaire au diamètre [AB] de (C), est tangente en B à ce cercle.

6. Calculons l'angle (, ) = (, ) + (, ) [mod π].

Les angles inscrits sont égaux à la moitié de l'angle au centre :
(, ) = (, ) [mod π],
(, ) = (, ) [mod π].

Dans la similitude A est point fixe, O a pour image O’, M a pour image M’, par conservation des angles on a (, ) = (, ) [mod π].
D'où – (, ) = (, ) et (, ) = 0 [mod π] ce qui prouve l'alignement.

Figure interactive dans GeoGebraTube : recherche d’un point fixe

Compétences évaluées
  • Réaliser des constructions avec un logiciel de géométrie dynamique.
  • Visualiser le lieu d'un point.

81. Aire variable d'un triangle

Situation
À partir de la courbe représentative d'une fonction numérique, on définit un triangle variable dans le plan.
On cherche à optimiser l'aire de ce triangle.

Énoncé

Soit un repère orthonormal (O, , ) du plan et la courbe C d'équation y = e^x − 1.
Soit B le point de C d'abscisse 1, et A le point de C d'abscisse a, a étant un nombre réel de l'intervalle [0 ; 1].
On s'intéresse à l'aire du triangle OAB et à la variation de cette aire en fonction de a.

Partie A

1. Construire la figure à l'aide d'un logiciel de géométrie dynamique.

2. Afficher à l'écran l'aire du triangle OAB.
En faisant varier a, chercher une valeur approchée de la valeur de a pour laquelle l'aire du triangle OAB est maximale.
Donner une valeur approchée de cette aire maximale.

3. Pour tout a dans l'intervalle [0; 1], on note f (a) l'aire du triangle OAB. Construire l'ensemble des points M(a ; f(a)).
Retrouver les résultats de la question précédente.

Partie B

4. (a) Déterminer l'expression de f(a) en fonction de a.
(b) En étudiant la fonction f, déterminer la valeur exacte de la variable a pour laquelle la fonction f atteint son maximum et la valeur exacte de ce maximum.

Production demandée

• Visualisation à l'écran de la figure demandée et de l'ensemble des points M de la question 3.
• Affichage des valeurs approchées de a et de f(a) pour lesquelles l'aire du triangle est maximale.
• Démarches et réponses argumentées à la question 4.

Compétences évaluées
Compétences TICE

• Utilisation d'un logiciel de géométrie pour construire une figure dans le plan ;
• Utilisation de l'aspect dynamique du logiciel pour établir des conjectures.

Compétences mathématiques

• Calcul de l'aire d'un triangle dont on connaît les coordonnées des sommets ;
• Détermination du maximum d'une fonction.

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Technique GeoGebra

Placer les points O et P(1, 0). Sur le segment [OP], placer le point N et nommer a le segment [ON].

La fonction g(x) = e^x − 1 sur l'intervalle [0, 1] est définie par Fonction[e^x − 1, 0, 1].

L'aire f du triangle est définie par Aire[O, A, B].

Pour rendre lisible le graphe de f des points M(a ; f(a)) on le décale et on le dilate par (a + 1.2, 10 f) et on trace le lieu du point M avec N comme pilote.

Télécharger la figure GeoGebra aire_triangle.ggb

83. Optimisation en géométrie plane

Situation
On propose, dans le plan muni d'un repère orthonormal, de déterminer la distance d'une courbe à une droite.
L'utilisation d'un logiciel de géométrie dynamique permet de formuler une conjecture qui sera ensuite démontrée.

Énoncé

Dans un repère orthonormal du plan, on considère la courbe représentative C de la fonction x → e^x et la droite D d'équation y = 2x − 3.
On se propose de déterminer, s'il existe, un point M de C tel que la distance de M à la droite D soit minimale.

Partie A

1. Utiliser un logiciel de géométrie pour construire la droite D et la courbe C.

2. Placer un point mobile M sur C et construire le point N image de M par la projection orthogonale sur D.

3. Conjecturer, au moyen du logiciel, l'abscisse du point M₀ de C dont la distance à D est minimale.
Proposer une valeur approchée de cette distance minimale.
Conjecturer une propriété de la tangente en M₀ à C.

Partie B

4. Élaborer une méthode permettant de démontrer ces conjectures.

5. Calculer les coordonnées de M₀ et sa distance à D.

Production demandée

• Construction de C, D, M et N au moyen du logiciel de géométrie.
• Conjectures relatives à l'abscisse de M₀ et à la tangente en M₀ à C.
• Proposition d'une valeur approchée de la distance de M₀ à D.
• Calcul des coordonnées de M₀ et de sa distance à D.

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Technique GeoGebra

Déplacer le point P, dans l'intervalle [P₂P₁], ce qui détermine l'abscisse a de M.

Pour tracer le projeté orthogonal N de M sur D, tracer le symétrique M’ de M par rapport à D, N est alors le milieu de [MM’].
Le lieu du point Q(a, MN) permet de trouver le minimum.

Indications

3. La distance minimale est obtenue pour un point d'abscisse x₀ ≈ 0,69.
La distance minimale est M₀N₀≈1,67.
La tangente t en M₀ à C est parallèle à la droite D.

4. La démonstration, basée sur la propriété de la convexité de la courbe exponentielle, est analogue à celle utilisée dans distance d'une courbe à un point.
Pour un point M sur C, le segment [MN] coupe la tangente D en M₁.
MN = MM₁ + M₁N = MM₁ + M₀N₀. MN est donc supérieur ou égal à M₀N₀, qui bien la distance minimale.

5. La pente de la tangente t est égale à 2, coefficient directeur de la droite D, donc e^x = 2 soit x₀ = ln(2) et M₀ a pour coordonnées (ln(2), 2).

Rappel de cours de 1^ère S : la distance d'un point M(x₀, y₀) à la droite d'équation ax +by + c = 0 est égale à .

Pour le point M₀(ln(2), 2) et la droite D d'équation 2x − y − 3 = 0, on a donc une distance minimale de , conforme au calcul de GeoGebra.

Télécharger la figure GeoGebra distance_droite_courbe.ggb

Compétences évaluées
Compétences TICE

• Tracer, dans un repère orthonormal, au moyen d'un logiciel de géométrie, des courbes définies par leur équation ;
• Construire l'image d'un point par une projection orthogonale.

Compétences mathématiques

• Connaître la définition de la projection orthogonale sur une droite ;
• Exprimer, en repère orthonormal, la distance d'un point à une droite ;
• Caractériser la tangente en un point à la courbe représentative d'une fonction dérivable ;
• Déterminer un extremum d'une fonction dérivable.

91. Propriétés de la courbe représentative d'une fonction

Énoncé

Soit f  la fonction définie sur R par : f(x) = − x + .
On note C sa courbe représentative dans le plan muni d'un repère orthogonal (O, , ).
Soit a un réel quelconque, M et N les points de C d'abscisses respectives a et − a.

1. Construire la figure à l'aide d'un logiciel de votre choix.

2. Faire varier a et émettre des conjectures concernant respectivement :

• la droite (MN) ;
• le lieu du point I intersection des tangentes à C en M et N.

3. On se propose d'étudier les conjectures émises à la question précédente.
(a) Déterminer en fonction de a les coordonnées des points M et N.
(b) Justifier les conjectures émises à la question 2.

Production demandée

• Visualisation à l'écran du lieu du point I.
• Réponses argumentées aux questions 3.(a) et (b).

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Indications

La droite (MN) a une direction fixe (coefficient directeur −1).
Le point I décrit le segment [0, 2] sur l'axe Oy.

Télécharger la figure GeoGebra secante_2_tangentes.ggb

128. Étude de la courbe représentative d'une fonction

Énoncé

On considère la fonction f définie sur l'intervalle [0; 1] par f(x) = (1 – )².
Soit C la courbe représentative de f dans le plan rapporté à un repère orthonormal.
On se propose d'établir une propriété de la courbe C.

1. (a) Représenter la courbe C à l'aide d'un outil de géométrie dynamique.
(b) Tracer la courbe représentative de la fonction g définie sur [0; 1] par g = f ° f puis conjecturer une expression simple de g(x), pour tout x appartenant à [0; 1].

2. (a) Placer un point M sur la courbe C, puis construire le point M’ symétrique de M par rapport à la droite D d'équation y = x.
(b) Quel semble être le lieu du point M’ lorsque M décrit la courbe C ?
(c) Quelle propriété de la courbe C peut-on alors conjecturer ?

3. (a) Pour tout réel x appartenant à l'intervalle [0; 1], exprimer f ° f (x) en fonction de x.
(b) En déduire la propriété de la courbe C observée à la question 2.(c).

Production demandée

    – Réalisation du graphique et construction pour observation du lieu du point M’.
    – Démarche de démonstration pour les questions 3.(a) et 3.(b).

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java.

Indications

1. (b) Pour tout x appartenant à [0; 1], g(x) = x.

2. (b) Lorsque M décrit la courbe C, le lieu de M’ est la courbe C.
La courbe C est symétrique par rapport à la droite D : f est égale à sa fonction réciproque f ^{– 1}.

3. (a) Pour tout x appartenant à [0; 1],

f ° f(x) = (1 – ]² = [1 − (1 – )]² = []² = x.

f ° f = Id ; f ^{– 1} = f. La courbe C est symétrique par rapport à la droite D.

Télécharger la figure GeoGebra fonction_auto_reciproque.ggb

131. Étude d'une figure du plan (spécialité)

Situation
L'objectif de l'exercice consiste à étudier une configuration géométrique plane à l'aide de similitudes directes.

Énoncé

Soit un triangle équilatéral direct ABC et soit D un point du segment [BC]. La parallèle à la droite (AC) menée par D coupe la droite (AB) en E et la parallèle à la droite (AB) menée par D coupe la droite (AC) en F. Soit le point G, centre de gravité du triangle ABC et les points H et A’, symétriques de G et A par rapport à la droite (BC). On définit les points I et J centres de gravité respectifs des triangles BDE et CDF.

On se propose d'étudier la nature du triangle HIJ quand D décrit le segment [BC].

1. (a) Représenter la figure à l'aide d'un logiciel de géométrie dynamique.
(b) Quelle semble être la nature du triangle HIJ ?
(c) Visualiser les lieux des points I et J lorsque le point D décrit le segment [BC].

Appeler l'examinateur pour une vérification de la figure réalisée.
Lui proposer les conjectures émises concernant le triangle HIJ et les lieux des points I et J.

2. On définit les similitudes directes S₁, de centre C, de rapport , d'angle et S₂, de centre B, de rapport = , d'angle
et leur composée f = S₂ ° S₁.

(a) Déterminer les images de J et H par f.
(b) Déterminer la nature et des éléments caractéristiques de f.
(c) En déduire la nature du triangle HIJ.

Production demandée

  • Réalisation de la figure.
  • Réponse argumentée à la question 2.

Compétences évaluées
  • Construire une figure à l'aide d'un logiciel de géométrie dynamique.
  • Visualiser un lieu de points et émettre une conjecture sur sa nature.
  • Utiliser des notions de géométrie élémentaire dans le plan : centre de gravité, longueur de la hauteur d'un triangle équilatéral…
  • Connaître les propriétés des similitudes (notamment, leurs composées).

Indications

Désolé, l'applet GeoGebra ne peut pas démarrer, vérifier votre version Java. Ce problème est un cas particulier du triangle de Napoléon, lorsque le triangle BCD est dégénéré. Il était traité, grâce à une rotation, dans la page : problème du BOA.

Trouver les médianes [BG] et [CG] comme lieu de points est très élémentaire !

Le point H est le centre de gravité du triangle équilatéral A’BC.

1. (b) Le triangle HIJ semble équilatéral.

(c) Le point I situé sur la médiane issue de B du triangle équilatéral BDE est situé sur la médiane [BG] du triangle ABC. Avec GeoGebra, on visualise le lieu de I qui est le segment [BG] et celui de J le segment [CG], ce qui permet de préparer la question suivante. À l'issue de cette question 2.(a), on pourra affirmer que ces lieux, images du segment [BC] par les similitudes S₁ et S₂^{– 1}, sont exactement les segments [GC] et [BG].

2. (a) D'après les propriétés métriques du centre d'un triangle équilatéral, la distance de ce centre à un sommet est égale à la longueur du côté du triangle divisé par .
L'image par S₁ du centre de gravité d'un triangle équilatéral de sommet C est un deux autres sommets.
Par S₂ l'image d'un des sommets d'un triangle équilatéral de sommet B est le centre de gravité de ce triangle.
Donc par S₁ : J a pour image D et H a pour image A’.
Réciproquement par S₂ : D a pour image I et A’ a pour image H.
Par la similitude f, l'image de J est I et H est un point fixe, f a pour centre H.

(b) La composée des similitudes S₁ et S₂ est une similitude de rapport le produit
× = 1 et d'angle le somme des angles + = . f est donc une rotation d'angle .

(c) Par la rotation f, de centre H, [HJ] a pour image [HI], donc HJ = HI et le triangle isocèle HIJ, ayant un angle de radians, est équilatéral.

Télécharger la figure GeoGebra triangles_equilateraux.ggb

Page n^o 133, créée le 16/08/2009
mise à jour le 16/9/2009