René Descartes Descartes et les Mathématiques

Tangente à une courbe

Mathématiques en 1^ère S avec GéoPlan :
calcul du coefficient directeur d'une droite (AM) et définition de la tangente par position limite.

Définir une tangente à la parabole

Utilisation de GéoPlan pour définir une tangente à la parabole (P) d'équation f(x) = x²

Créer la fonction x → x²
Utiliser le menu déroulant : créer > numérique> fonction numérique.
Taper x^2 pour obtenir le carré et nommer la fonction f. La fonction est alors définie.
Pour obtenir la représentation dans un repère orthonormal faire apparaître le repère avec la touche .
Dans le menu Éditer, appeler Éditer texte figure ;
changer la position du repère (O, , ) en modifiant les valeurs des extrema :
Position de Roxy: Xmin: -0.25, Xmax: 1.25, Ymax: 1.4 et exécuter.
Tracer la fonction f sur l'intervalle [-3, 3] :
Menu ligne courbe > Graphe d'une fonction prédéfinie (pour l'intervalle, ne taper que les deux valeurs des extrémités).
Créer le point A(1, f(1)) à l'aide d'une variable a, affectée à 1 :
Menu Créer > variable réelle libre a dans l'intervalle [-3, 3]
Menu Piloter > affecter une valeur à une variable numérique : a affectée à 1
Créer le point repéré A(a, f(a)).
Créer le point M(a+h, f(a+h)) à l'aide d'une variable h :
Menu Créer >variable réelle libre h dans l'intervalle [-1, 1]
Créer le point repéré M(a+h, f(a+h)).
Créer la sécante (AM) :
Menu Créer > Ligne > Droite > Définie par deux points.
Déplacer le point M
choisir piloter au clavier la variable h.
Touches ↑ ou ↓ pour déplacer le point M ;
touches + ou - pour régler le pas.
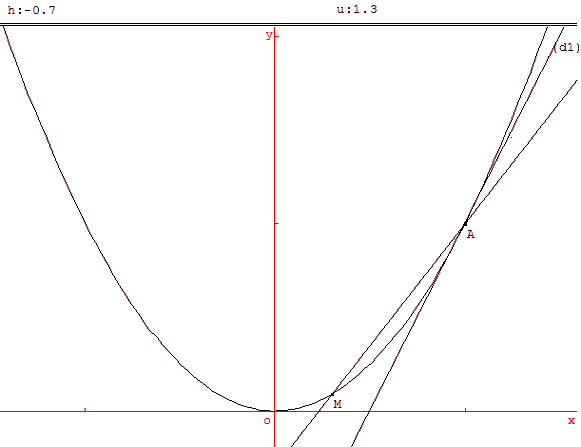
Observer le comportement de la sécante (AM) lorsque M est proche de A. Faire des zooms.
Calculer le coefficient directeur de la droite (AM) :
Créer calcul algébrique (f(a+h) - f(a))/h a affecter dans la variable numérique u
Créer l'affichage des variables numériques h et u.
Lorsque M tend vers A, observer le coefficient directeur de (AM).
La droite (d₁) est la limite de la droite (AM) lorsque M tend vers A.
Créer cette droite : Menu Ligne : droite ; Point - coefficient directeur (la nommer d₁).

corde et tangente - copyright Patrice Debart 2003

Télécharger la figure GéoPlan tangente.g2w

Utilisation de l'éditeur du texte de la figure

tangente dr pente 2 - copyright Patrice Debart 2003

Terminer par exécuter

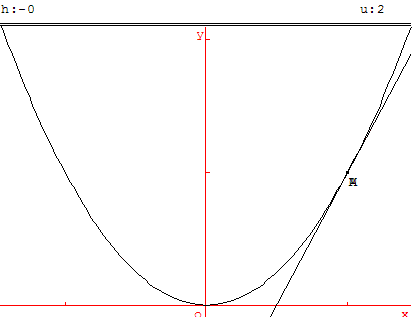
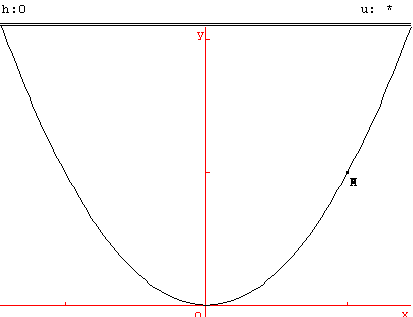
Remarque : pendant la phase de recherche, on peut suivant l'initialisation des variables tomber sur l'une ou l'autre des situations ci-contre ou ci-dessous, avec exactement les mêmes programmes. Bonne occasion pour une explication sur les limites et les calculs faits par l'ordinateur.