Descartes et les Mathématiques

Constructions de perpendiculaires et de parallèles

Dix-sept exercices pour illustrer diverses méthodes de constructions de perpendiculaires ou parallèles, menées à une droite à partir d'un point donné.

Tracer une perpendiculaire

1. Perpendiculaire abaissée d'un point sur une droite

2. Perpendiculaire élevée d'un point à une droite

Tracer une parallèle

Parallèle à une droite passant par un point donné
    3. Constructions avec compas
    4. Constructions avec règle et milieu

5. Parallèle à une droite située à une distance donnée

Diverses constructions, à la règle et au compas, des perpendiculaires ou parallèles, menées à une droite (d) donnée, à partir d'un point M donné.

Pour tracer des droites parallèles ou perpendiculaires à la « règle et au compas », il faut souvent se ramener à la construction de la médiatrice d'un segment.

Construction de droites perpendiculaires au compas

1. Perpendiculaire abaissée d'un point sur une droite

Comment tracer une perpendiculaire au compas ?

Ci-dessous deux constructions de la perpendiculaire à une droite (d) donnée, abaissée d'un point M donné, extérieur à (d).
Pour cela, à partir de deux points A et B de la droite (d), tracer les deux cercles, passant par M, ayant comme centres ces deux points A et B.
Ces cercles se recoupent en N qui est le symétrique de M par rapport à (d). La droite (MN) est la perpendiculaire cherchée.

1.a. Construction au compas de la médiatrice d'un segment [AB] de (d)

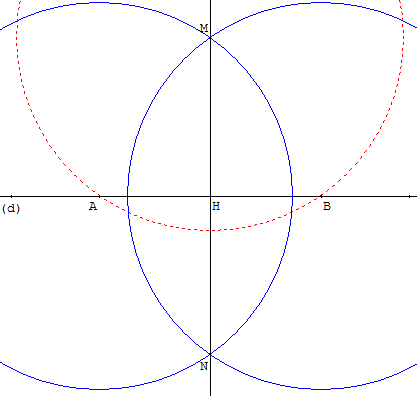
Soit une droite (d) et un point M à l'extérieur de (d).

Un cercle de centre M rencontre la droite (d) en A et B.
Deux autres cercles de même rayon de centres A et B passent par M et se recoupent en N.
La perpendiculaire, à (d), est la droite (MN).

Télécharger la figure GéoPlan perpendiculaire_abaissee_1.g2w

1.b. Deux cercles, passant par M, centrés sur (d)

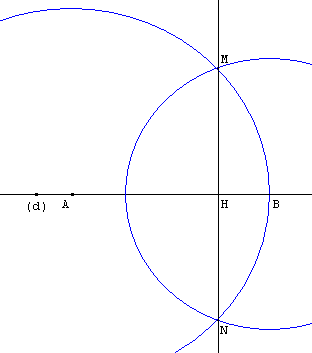
Un point A de la droite (d) est le centre d'un cercle passant par M.
Il rencontre (d) en B. Le cercle de centre B passant par M rencontre le premier cercle en N.

La perpendiculaire est la droite (MN).

Remarque :
Il est possible de remplacer B par n'importe quel point de (d), distinct de A.

Télécharger la figure GéoPlan perpendiculaire_abaissee_2.g2w

1.c. Configuration : médiane d'un triangle isocèle

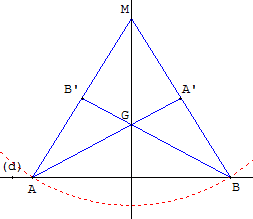
Dans la figure ci-dessus, un cercle de centre M coupe (d) en A et B.
AMB est un triangle isocèle de base [AB] : la hauteur issue de M est aussi médiane.

Avec le compas, il est possible de tracer les milieux A’ de [MB] et B’ de [MA].
Les deux médianes [AA’] et [BB’] se coupent au centre de gravité G.

La troisième médiane (AG) est perpendiculaire à la base.
C'est la perpendiculaire cherchée.

Télécharger la figure GéoPlan perpendiculaire_abaissee_3.g2w

1.d. Construction avec un cercle

Cercle ayant un diamètre dont les extrémités sont M et A, un point de (d)

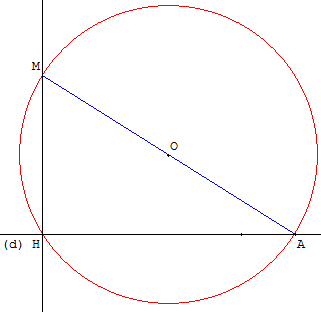
Placer un point A sur la droite (d). Le cercle de diamètre [AB] recoupe la droite (d) en H.
Le triangle AMH, inscrit dans un demi-cercle, est rectangle et la droite (MH) est la perpendiculaire cherchée.

Télécharger la figure GéoPlan perpendiculaire_abaissee_4.g2w

1.e. Configuration : hauteur d'un triangle, voir construction à la règle seule (avec un cercle)

2. Perpendiculaire élevée d'un point à une droite

Perpendiculaire élevée d'un point A à une droite (d)

2.a. Tracé d'une médiatrice

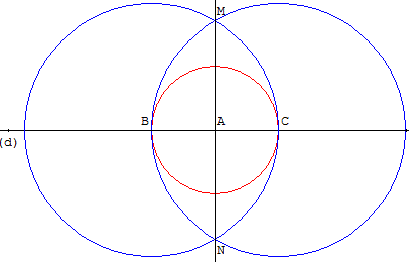
Dessiner une médiatrice d'un segment [BC] ayant A comme milieu

Soit une droite (d) et un point A sur (d).

Un cercle de centre A rencontre (d) en B et C.

Tracer la médiatrice de [BC] grâce aux cercles de centre A passant par B et de centre B passant par A.
Ces deux cercles se coupent en M et N.

La perpendiculaire est la droite (MN).

Télécharger la figure GéoPlan perpendiculaire_elevee_1.g2w

2.b. Tracé d'un cercle par son diamètre

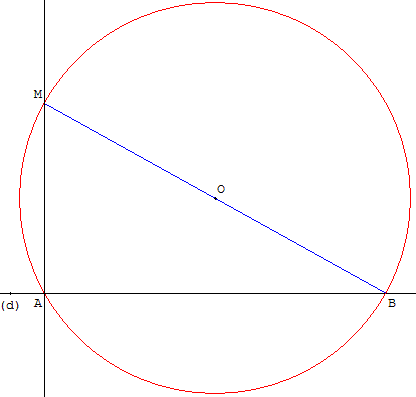
Même figure que celle de la construction d'une perpendiculaire abaissée d'un point M, en changeant l'ordre des tracés.

Soit une droite (d) et un point A sur (d).

À partir d'un point O hors de (d), tracer un cercle de centre O, passant par A. Si le cercle est tangent en A à la droite, le point O est sur la perpendiculaire cherchée qui est la droite (OA), sinon le cercle recoupe (d) en un deuxième point B. Tracer la droite (BO) qui recoupe le cercle en M.

Le point M, symétrique de B par rapport à O, est diamétralement opposé à B.

La droite (AM) est la perpendiculaire à (d) cherchée.

Explications : Le triangle BAM, inscrit dans un demi-cercle, est rectangle en A.

Télécharger la figure GéoPlan perpendiculaire_elevee_2.g2w

2.c. Tracé d'une perpendiculaire en bout

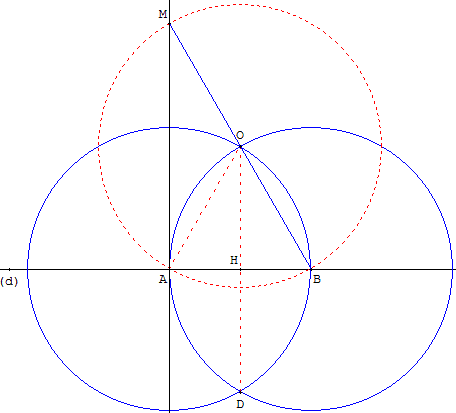
Tracer un cercle de centre A qui rencontre (d) en B, puis avec le même rayon, un cercle de centre B passant par A, qui rencontre le premier cercle en O.
Tracer le point M, symétrique de B par rapport à O.
La perpendiculaire à (d) est (AM).

Explications : toujours avec le même rayon AO, tracer un troisième cercle de centre O, passant par A et B, le deuxième point d'intersection de ce dernier cercle et de la droite (BO) est le point M.
Le triangle BAM, inscrit dans un demi-cercle, est rectangle en A.

Autre point de vue : perpendiculaire abaissée et droite des milieux
À partir d'un point O hors de (d), avec un cercle de centre O, passant par A, on retrouve alors le tracé de la perpendiculaire (OH) abaissée d'un point O.
Tracer le point M, symétrique de B par rapport à O.
Le théorème des milieux permet de justifier la construction : dans le triangle ABM, (OH) est une droite des milieux : (AM) est parallèle à (OH).
(OH) est perpendiculaire à (d), donc (AM) est perpendiculaire à (d).

Télécharger la figure GéoPlan perpendiculaire_elevee_3.g2w

Construction de droites parallèles au compas

3. Parallèle à une droite par un point donné

Proposition 31 du livre I des Éléments d'Euclide : par un point donné, construire une ligne parallèle à une droite donnée.

L'unicité se déduit du postulat 5 : si une droite, tombant sur deux droites, fait les angles intérieurs d'un même côté plus petits que deux droits, ces droites, prolongées à l'infini, se rencontreront du côté où les angles sont plus petits que deux droits.

Ce postulat est par la suite plus souvent énoncé sous la forme : « Par un point il passe une et une seule parallèle à une droite donnée ».

Construction au compas de la parallèle à une droite (d) passant par un point M extérieur

3.a. Construction de deux cercles

Tracer une droite parallèle au compas

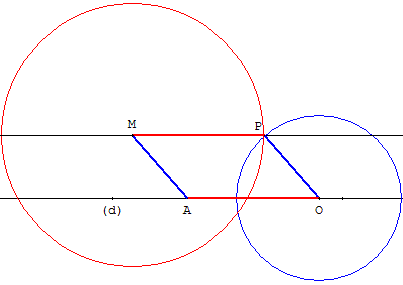
Soit une droite (d) et, à l'extérieur de (d), un point M.

Placer deux points A et O sur la droite (d).

Tracer le cercle de centre O de rayon AM et le cercle de centre M et de rayon AO.

Soit P un des points d'intersection des deux cercles, convenablement choisi.

Le quadrilatère AMPO a ses côtés opposés de longueurs égales, deux à deux.
C'est un parallélogramme.

La droite (MP) est la parallèle à (d) cherchée.

Télécharger la figure GéoPlan parallele_8.g2w

3.b. Angles alternes-internes

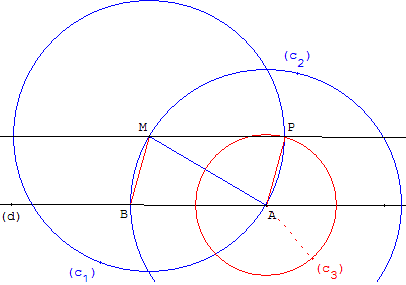
Soit une droite (d), un point A sur (d) et un point M.

La droite (d) et la parallèle (d’) à (d) passant par un point M doivent faire avec une sécante (AM) des angles alternes-internes BMA et MAP égaux entre eux.

Pour cela :

Tracer le cercle (c₁) de centre M passant par le point A de la droite (d),
puis le cercle (c₂) de centre A passant par M.
Le cercle (c₂) coupe la droite (d) en B.

Pour reporter l'angle BMA en A, reporter l'arc MB de (c₂) sur le cercle (c₁).
Tracer le cercle (c₃) de centre A et de rayon BM. Choisir pour P, le point d'intersection des cercles (c₁) et (c₃) situé du même côté que A par rapport à (d).

La droite (MP) est la parallèle cherchée.

Télécharger la figure GéoPlan parallele_5.g2w

3.c. Dessiner un cercle avec son diamètre

Cercle M ayant un diamètre dont les extrémités sont M et A, un point de (d)

Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles :
on répète donc deux fois la construction afin d'obtenir « la perpendiculaire d'une perpendiculaire ».

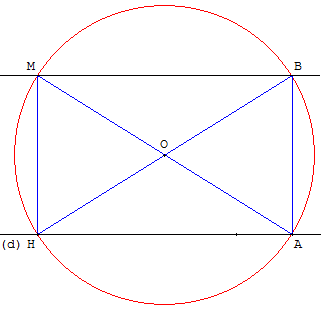
Commencer par la construction de la perpendiculaire à une droite (d), abaissée d'un point M.

Placer un point A sur la droite (d). Le cercle de diamètre [AB] recoupe la droite (d) en H.
Le triangle AMH, inscrit dans un demi-cercle, est rectangle et la droite (MH) est perpendiculaire à (d).

Soit B le symétrique de H par rapport au centre O du cercle, deuxième intersection du cercle avec la droite (AO).

MHAB est un rectangle et la droite (MB) est la parallèle à (d) cherchée.

Télécharger la figure GéoPlan parallele_10.g2w

3.d. Deux médiatrices

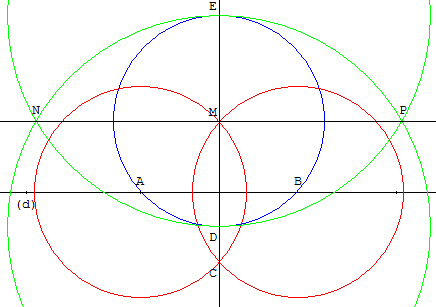
Il est possible d'utiliser deux fois la construction de la médiatrice pour tracer la « perpendiculaire d'une perpendiculaire »

Soit une droite (d) et un point M extérieur.

Construire une médiatrice (MC), passant par le point M, d'un segment [AB] de (d), puis tracer une deuxième médiatrice d'un segment [DE] de la droite (MC).

Pour cela, choisir un point A sur (d).

Un cercle (c₁) de centre M, passant par le point A de la droite (d), recoupe cette droite en B.
Les cercles de centres A et B passant par M se recoupent en C. La droite (MC), médiatrice de [AB], est perpendiculaire à (d).

Le cercle (c₁) coupe (MC) en D et E. Les cercles de centre D passant par E et de centre E passant par D se coupent en N et P.
La droite (NP), médiatrice de [DE], est la parallèle à (d) passant par M.

Télécharger la figure GéoPlan parallele_4.g2w

3.e. Construction avec deux ou trois cercles

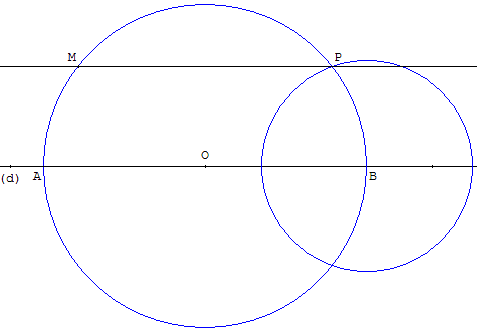
Construire un trapèze isocèle AMPB

Soit une droite (d), un point O sur (d) et un point M.

Le cercle (c) de centre O, passant par M, coupe la droite (d) en A et B. Mesurer, avec le compas, la longueur AM et tracer le cercle de centre B et de rayon AM. Ce dernier cercle rencontre (c) en P situé dans le même demi-plan que le point M par rapport à (d).

La droite (MP) est parallèle à (d).

Télécharger la figure GéoPlan parallele_1.g2w

Tracer un losange AMPB

Soit une droite (d), un point A sur (d) et un point M.

Tracer trois cercles de même rayon AM.

Un premier cercle (c₁) de centre M, passant par un point A de (d).
Le deuxième de centre A, passant par M, rencontre (d) en B situé à l'extérieur de (c₁).
Le troisième de centre B, passant par A, recoupe le premier en P.

La droite (MP) est parallèle à (d).

Télécharger la figure GéoPlan parallele_2.g2w

3.f. Construction avec deux cercles tangents

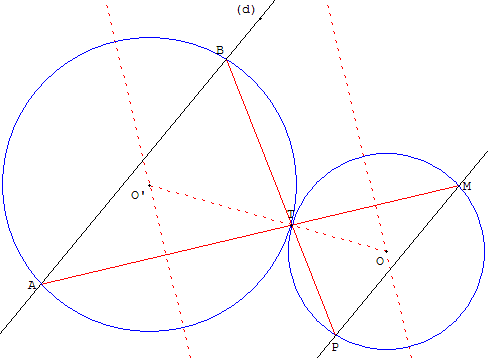
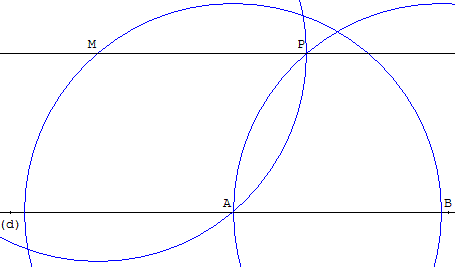
Soit une droite (d), un point A sur (d) et un point M.

Utiliser la configuration des cordes de cercles tangents :
Placer un point A sur la droite (d) et un point T sur le segment [AM].
Tracer deux cercles tangents en T passant par A pour l'un, par M pour l'autre.

Pour cela, placer un point O sur la médiatrice de [TM]
et tracer le cercle (c) de centre O, passant par M et T.

La droite (OT) coupe la médiatrice de [AT] en O’. Le cercle (c’) de centre O’ passant par T et A est tangent en T au cercle (c).

Ce cercle recoupe la droite (d) en B.
La droite (BT) recoupe le cercle (c) en P.

La droite (MP) est la parallèle à (d) passant par M.

Télécharger la figure GéoPlan parallele_7.g2w

4. Tracés de droites parallèles

À la règle, avec milieu

Il est démontré qu'il impossible avec uniquement une règle :
    – de construire le milieu d'un segment,
    – de mener par un point une parallèle à une droite.

Si on donne deux droites parallèles, alors il est possible de tracer de la parallèle à ces deux droites, passant par un point extérieur, seulement avec la règle.

Il est aussi possible de tracer une parallèle avec une règle à bords parallèles.

4.a. Construction de Hilbert

Parallèle construite avec règle et milieu

Grundlagen der Geometrie

Construction avec règle et instrument (« Eichmass » permettant de reporter une longueur).

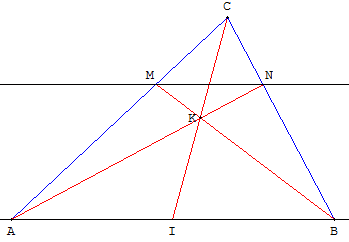
– Placer deux points A et B sur la droite (d)
– Tracer le milieu I de [AB].
– Placer un point C sur la demi-droite [AM).
– Mener deux droites (CI) et (BM) qui se coupent en K.
– La droite (AK) coupe (BC) en N.

– La droite (MN) est la parallèle à (d) cherchée.

Démonstration (au-delà du lycée)

Si les droites (AB) et (MN) étaient sécantes, elles le seraient en un point J tel que
[A, B, I, J] = - 1 forment une division harmonique.

Mais dans une relation de division harmonique, si le troisième point est le milieu des deux premiers, alors le quatrième point J est à l'infini.
Les droites sont donc parallèles.

Télécharger la figure GéoPlan para_regle_milieu.g2w

Réciproque : construire un milieu avec deux parallèles

Droite des milieux

4.b. Recherche d'une « droite des milieux » avec GéoPlan

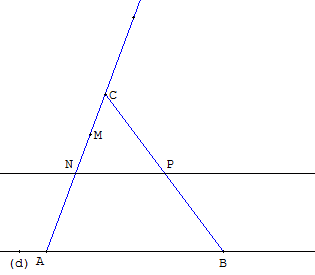
Placer deux points A et B sur la droite (d).

Placer un point variable C sur la demi-droite [AM].
Soit N et P les milieux des côtés [AC] et [BC].
La droite des milieux (NP) est parallèle à (d).

Déplacer le point C jusqu'à ce que le point N coïncide avec M.

Remarque : déplacer un point sur l'écran pour qu'il coïncide avec un autre point fixe, avec pour seul moyen de contrôle la perception visuelle, peut suffire dans un premier temps.
Cette utilisation approchée du logiciel est qualifiée de « molle »

Nous pouvons conjecturer que la solution a lieu quand le point C est le symétrique de A par rapport à N.

Avec GéoPlan, la touche S réalise une figure exacte par l'affection directe du point libre C au point O, symétrique de A par rapport à N.
Parfois nous nous contenterons de cette « preuve par GéoPlan », utilisation « dure » du logiciel.

Télécharger la figure GéoPlan parallele_12.g2w

La parallèle comme « droite des milieux » d'un triangle
Tracé à partir de trois points équirépartis sur (d)

Classe de quatrième

Pour cet exercice, la justification géométrique ci-dessous, est accessible dès la classe de quatrième.

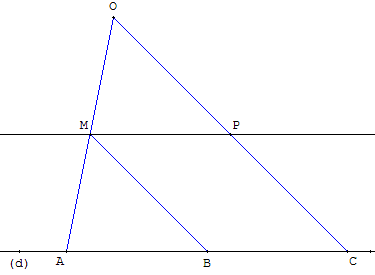
Placer deux points A et B sur la droite (d). Tracer le symétrique C de A par rapport à B. B est alors le milieu de [AC].

Sur la droite (AM), placer le symétrique O de A par rapport à M tel que MO = AM,
Sur la segment [CO], placer le milieu P. Cette construction se fait au compas en reportant la longueur BM sur [CO].

La droite (MP) est la parallèle à (d) cherchée.

En effet, (BM) et (MP) sont les droites des milieux du triangle OAC.

Télécharger la figure GéoPlan parallele_9.g2w

4.c. La droite (d) comme « droite des milieux » d'un triangle
Tracé à partir de deux points sur (d)

Accompagnement du programme de 3^e - 2004

Placer deux points A et B sur la droite (d).

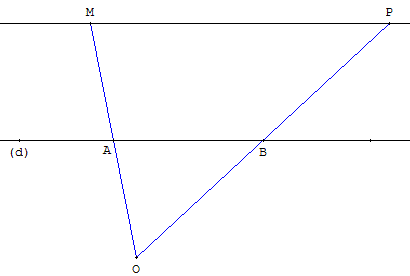
Sur la droite (AM), placer le symétrique O de M par rapport à A,
tel que AO = AM,
Sur la droite (OB), placer le symétrique P de O par rapport à B,
tel que BP = BO.

La droite (MP) est la parallèle à la droite (d) cherchée.

En effet, (AB) est une droite des milieux du triangle OMP :
(MP) est parallèle à (AB).

Télécharger la figure GéoPlan parallele_6.g2w

Voir aussi : géométrie en troisième

4.d. Configuration de Thalès

Tracé d'une droite limite, avec une figure analytique, non constructible à la règle et au compas.

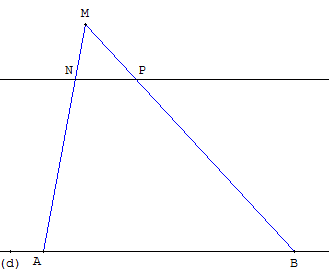
Placer deux points A et B sur la droite (d).

Placer un point variable N sur le segment [AM] construire, sur [BM], le point P tel que BP/BM = AN/AM.
Avec GéoPlan, si x est l'abscisse de N sur la droite repérée (A, M), alors le point P a pour abscisse x sur la droite repérée (B, M).

Par Thalès, la droite (NP) est parallèle à (d).

Déplacer le point N vers M.

La construction n'est pas réalisée lorsque N est en M, mais N peut être aussi proche que l'on veut de M et la droite (NP) a pour position limite la parallèle à (d) en M.

Télécharger la figure GéoPlan parallele_13.g2w

4.e. Approximations successives

Création itérative avec GéoPlan

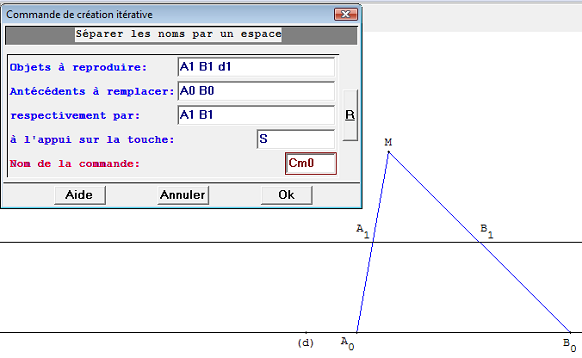
À la règle et au compas avec GéoPlan, il possible de réaliser la construction ci-dessus, à droite, de façon itérative par approximations successives de droites des milieux (x =, , 7/8…).

Construire une première droite des milieux d₁ = (A₁B₁) en utilisant deux points A₀ et B₀ de la droite (d) et le point M donné.

Pour la création itérative, nommer A₀ et B₀ les points de (d), A₁ et B₁ les milieux de [ A₀M] et [B₀M], d₁ la droite des milieux (A₁B₁).

Par appui de la touche S, GéoPlan reprend les deux milieux précédents et recommence l'application « droite des milieux ».

Toutes les droites successives, ainsi obtenues, sont parallèles entre elles et parallèles à la droite (d) donnée. À chaque étape, on se rapproche
de plus en plus du point M. On ne peut pas atteindre le point M, mais l'on peut en être aussi proche que l'on veut.

Télécharger la figure GéoPlan parallele_14.g2w

Droites des milieux - création itérative

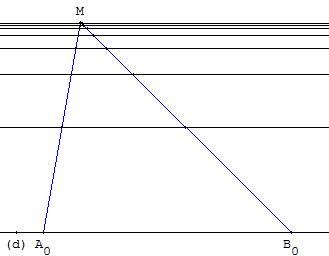
Droites des milieux d₁ à d₇.

Position limite

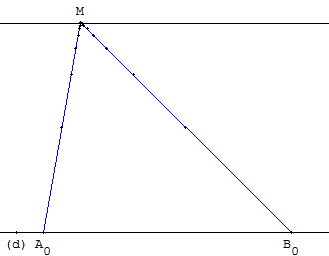
En 7 itérations, pour x =127/128, la droite d₇ semble passer par M.

4.f. Parallèle constructive avec règle et milieux

Avec une règle non graduée, la parallèle est constructible en utilisant la possibilité de tracer des milieux de segments.
Pour cela :

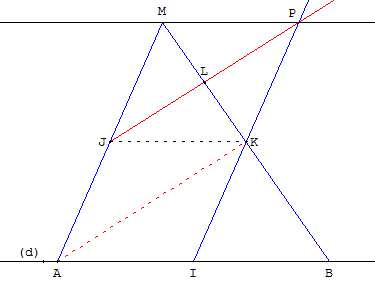
  – On place deux points distincts A et B sur la droite (d),
  – on trace les milieux I de [AB], J de [AM] et K de [BM],
  – on trace le milieu L de [KM],
  – on trace les droites (IK) et (JL) qui se coupent en P,
  – on trace la droite (MP) qui est la parallèle à la droite (d) passant par le point M, construite avec droites et milieux.

La démonstration géométrique est aisée pour les élèves de troisième ou de quatrième.
En effet, il s'agit d'utiliser des propriétés du parallélogramme et de la « droite des milieux ».

Télécharger la figure GéoPlan parallele_11.g2w

Le miroir des maths - Dr. Ruben Rodriguez Herrera

5. Parallèle à une distance donnée

Parallèle à une droite (D) située à une distance donnée d

À; partir d'un point A de la droite (D), tracer un cercle (c) de rayon donné d
Ce cercle coupe la droite en B et C.

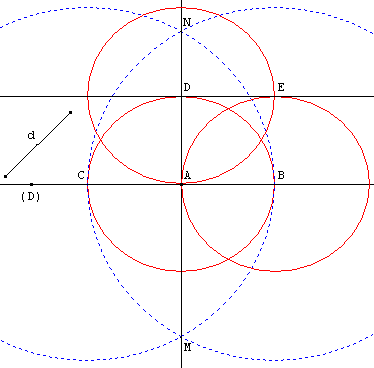
Utiliser la méthode du paragraphe 2 pour construire la médiatrice de [BC] grâce aux cercles de centre B passant par C et de centre C passant par B. Ces deux cercles se coupent en M et N. La droite (MN) est perpendiculaire en A à (D).

Soit D un des points où le cercle (c) coupe (MN) ; point situé à une distance d de A.

Les cercles de rayon d, passant par A, centrés en B et en D se coupent en E, quatrième sommet du carré DABE de côté d.

La droite (DE) est parallèle à la droite (D) et est située à la distance d.

Télécharger la figure GéoPlan parallele_3.g2w

Table des matières

Dans d'autres pages du site

Constructions uniquement à la règle :
    – une parallèle à deux droites parallèles

    – une parallèle avec une règle à bords parallèles

Constructions d'une parallèle avec une équerre

Histoire des mathématiques

Les Éléments d'Euclide

Les grands problèmes de la géométrie grecque

Médiatrice : construction d'Œnopide de Chio

Démonstrations géométriques de Pythagore

Cercles d'Apollonius

Rétrolien ( backlink)

Bateau-pompe – Embrun

Excellente manière que de tracer les perpendiculaires avec un compas, c'est même la seule méthode réellement juste.
Évidemment, pour des travaux mineurs une équerre reste utile.
Comme elle resterait indispensable à ceux qui auraient un caramel mou en lieu et place des cellules grises.
Pour info, voici ce qu'apprennent nos têtes blondes au collège.

Google friendly