Descartes et les Mathématiques

Constructions à la règle seule

Constructions uniquement à la règle non graduée, ou avec la règle et un cercle.

Sommaire

I. Constructions uniquement à la règle

1.1. Figure constructible à la règle seule

1.2. Symétrique d'un point par rapport à une droite

1.3. Parallèle à deux droites

1.4. La règle trop courte

II. Constructions à la règle et un cercle

2.1. Parallèle ou perpendiculaire à une droite sécante au cercle

2.2. Perpendiculaire abaissée d'un point sur une droite

I. Construction uniquement à la règle

1.1. Figure constructible à la règle seule

Des points de base étant donnés, un point est constructible à la règle s'il est point d'intersection de deux droites, chacune de ces deux droites passant par deux points, qui sont des points de base ou des points déjà construits.

Pour les constructions à la « règle et au compas », deux points de base suffisent.
À la règle seule, avec deux ou trois points de base, il n'est pas possible d'obtenir de nouveaux points.

Construction avec quatre points de base

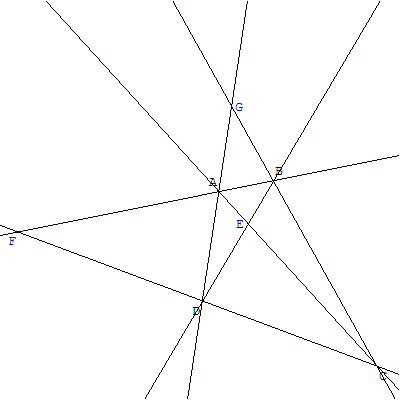
Première étape

On choisit quatre points A, B, C, D formant un quadrilatère autre qu'un trapèze.

On trace les six droites que les côtés du quadrangle permettent de définir.

Les intersections des paires de côtés opposés, permettent d'obtenir trois nouveaux points diagonaux : E, F, G.

Télécharger la figure GéoPlan quatre_pt_base_1.g2w

Deuxième étape

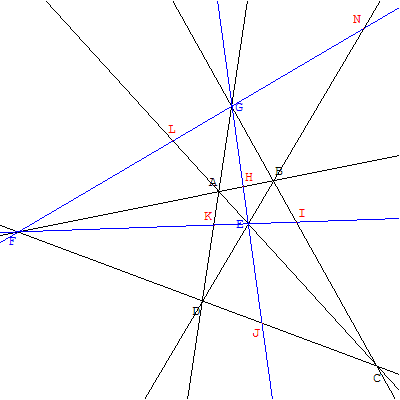
À partir des quatre points de base et des trois points d'intersection obtenus, on trace les trois nouvelles droites possibles.

On obtient six nouveaux points d'intersection : H, I, J, K, L, N.

Télécharger la figure GéoPlan quatre_pt_base_2.g2w

Troisième étape

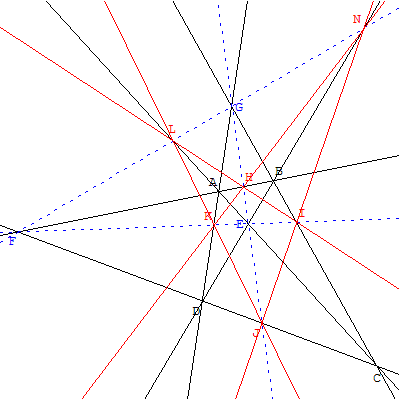
Les six points H, I, J, K, L, N sont alignés, trois à trois, sur quatre droites formant un quadrilatère complet.

Et ainsi de suite…

Télécharger la figure GéoPlan quatre_pt_base_3.g2w

Les propriétés d'une figure constructible à la règle sont conservées par projection centrale. Ce n'est pas le cas pour les milieux, les parallèles ou les symétries.
Il en découle qu'il est impossible, avec seulement une règle, de construire le milieu d'un segment ou de mener, par un point, une parallèle à une droite.

Les figures de la géométrie projective : quadrilatère complet, polaire, figures des théorèmes de Pappus et Desargues… sont constructibles à la règle seule ;

mais pas la droite de Newton, nécessitant la notion de milieu.

1.2. Symétrique d'un point par rapport à une droite

On donne une droite (d), les points A et B, non situés sur (d), ainsi que le point A’ symétrique de A par rapport à (d).

Construire le point B’ symétrique de B, par rapport à (d), en utilisant la règle seule.

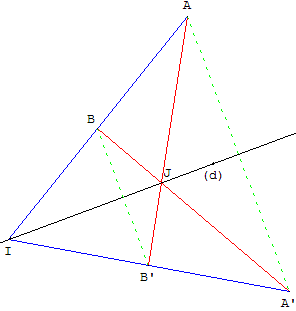
Solution

La droite (d) coupe (AB) en I et (A’B) en J.
Les droites (IA’) et (JA) se coupent en B’.
La droite (IA) a pour symétrique (IA’), la droite (JA’) a pour symétrique (JA).

Le point B, intersection de (IA) et (JA’) a pour symétrique l'intersection des images (IA’) et (JA), soit le point B’.

Remarques : cette solution nécessite que les droites (AB) et (AB’) ne soient pas parallèles à (d).

La construction permet aussi de trouver la perpendiculaire abaissée du point B sur la droite (d) : la droite (BB’).

Symétrique d'un point par rapport à une droite : voir règle à bords parallèles

Image expotée dans WikPédia : construction à la règle seule

Télécharger la figure GéoPlan sym_point.g2w

1.3. Par un point, droite parallèle à deux parallèles

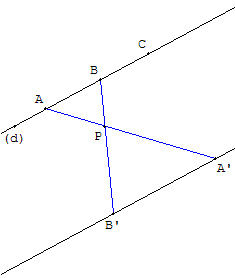
Construire une droite parallèle à deux droites (d) et (d’ ) parallèles, passant par un point donné

Si on donne le tracé deux droites parallèles, alors le tracé de la parallèle à ces deux droites, passant par un point extérieur, est possible uniquement avec la règle.

On donne deux droites parallèles distinctes (d) et (d’) et un point P n'appartenant pas à ces droites.
Construire la droite parallèle à (d) et (d’), passant par le point donné P, en n'utilisant que la règle.

Construction : P entre les deux droites

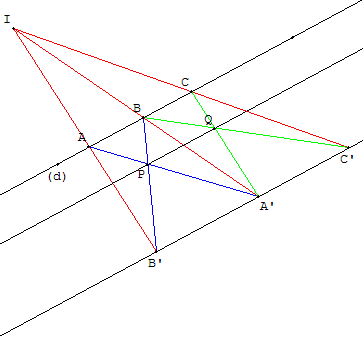
Solution

Méthode d'un faisceau de droites passant par un point I, le point I étant choisi de telle façon que le point P soit situé sur la polaire de I par rapport à (d) et (d’).

À partir de deux points A et B différents sur (d), tracer deux sécantes (AA’) et (BB’) passant par P avec A’ et B’ sur (d’).
Soit I le point d'intersection des droites (AB’) et (BA’).

Placer un point C, distinct de A et B, sur (d) et soit C’ l'intersection de (IC) avec (d’).
Les droites (BC’) et (CA’) se coupent en Q.

La droite (PQ) parallèle à (d) et (d’) est construite à la règle seule

P à l'extérieur des deux droites

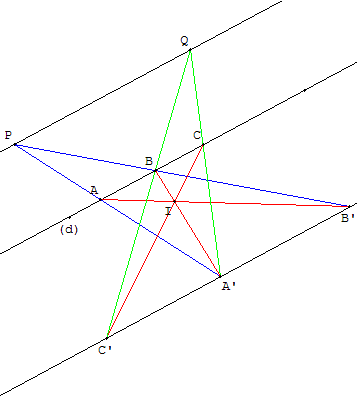
Remarques : si le point P est équidistant de (d) et (d’), les droites (AB’) et (BA’) sont parallèles et leur intersection est vide. Il faut tracer une autre parallèle : pourquoi pas la parallèle à (AB’) et (BA’) passant par C, point de (d) à l'extérieur du segment [AB]. Cette parallèle coupe (d’) en C’. Le centre Q du parallélogramme BCC’B’ permet de trouver la parallèle (PQ).

Avec la règle à bords parallèles seule, cette méthode permet de construire la parallèle à une droite donnée passant par un point donné : en plaçant un des bords de la règle sur la droite donnée (d), le deuxième bord permet de tracer (d’). Terminer la construction de la parallèle (PQ) passant par le point donné P comme ci-dessus.

Télécharger la figure GéoPlan para_2_droites.g2w

Images expotées dans WikPédia : construction à la règle seule

Droites (d) et (d’) concourantes :
    Construction par polaires réciproques : intersection inaccessible

    Texte historique de Jean-Henri Lambert

1.4. La règle trop courte

Joindre deux points d'une droite avec une règle trop courte.

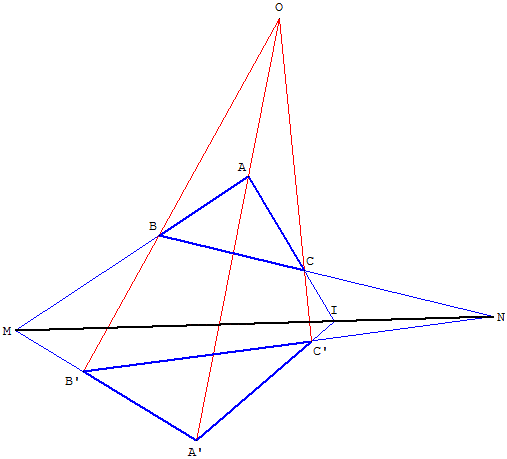
Pour tracer une droite (MN), avec une règle de longueur inférieure à MN, l'idée est de construire un point intermédiaire I grâce à une configuration de Desargues

que l'on a déjà rencontrée dans la construction d'une droite menée à partir du point de concours inaccessible.

Pour cela, placer convenablement deux points O et A, puis un point A’ sur la droite (OA).

On choisit un point B sur le segment [MA]. La droite (OB) coupe le segment [MA’] en B’.

On choisit un point C sur le segment [NB]. La droite (OC) coupe le segment [NB’] en C’.

Le point I intersection des droites (AC) et (A’C’) est le point intermédiaire cherché et le tracé de [MI] et de [IN] permet de dessiner le segment [MN].

Remarque : pour une règle de longueur l, cette construction permet tracer la droite (MN)
pour l < MN < 2l.

Si les points M et N sont plus espacés que le double de la longueur de la règle, en théorie il est possible de réitérer la construction de façon récursive en appliquant le procédé à des points intermédiaires I, J, K… etc.

Télécharger la figure GéoPlan droite_mi_desargues.g2w

Utilisation de l'espace pour un problème plan

La démonstration « par le relief » est facile en imaginant que les deux triangles ABC et A’B’C’ représentent deux triangles de l'espace non situés dans le même plan. Le point O est alors le centre d'une perspective transformant ABC en A’B’C’.
Les plans (ABC) et (A’B’C’) se coupent suivant une droite (d), qui s'appelle l'axe d'homologie.

Par construction, les droites (AB) et (A’B’) se coupent en M, les droites (BC) et (B’C’) se coupent en N.
La droite d'intersection (d), des deux plans, est donc la droite (MN).

Les droites (AC) et (A’C’) situées dans le plan (OAC) sont concourantes en un point I.
Le point I situé sur (AC) appartient au plan (ABC). I aussi situé sur (A’C’) appartient au plan (A’B’C’).

Le point I, contenu dans les plans (ABC) et (A’B’C’), est donc un point de leur droite (d) d'intersection.
Le point I est donc bien situé sur le segment [MN].

II. La règle et un cercle

Théorème de Poncelet-Steiner : en se donnant un cercle et son centre, avec uniquement une règle, on peut construire tout point constructible à la « règle et au compas », c'est-à-dire que l'on a la structure euclidienne.

2.1. Parallèle ou perpendiculaire à une sécante au cercle

On donne une droite (d), un point P et un cercle (c) de centre O. La droite (d), ne passe pas par le centre O et coupe le cercle en M et N.
Tracer la parallèle, ou bien la perpendiculaire, à (d) passant par P.

Solution

À l'aide des rayons (OM) et (ON), on construit à la règle les diamètres et le rectangle MNM’N’.
Le tracé de la droite (PQ) passant par P, parallèle ou perpendiculaire aux côtés du rectangle, se fait ensuite comme au paragraphe 1.4. ci-dessus.

Parallèle à (d) passant par P

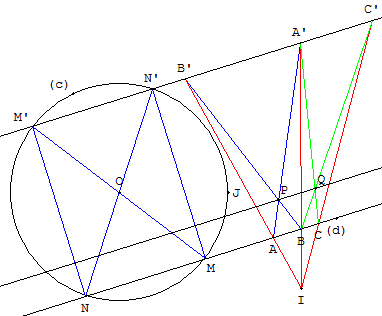
La donnée du cercle (c) permet de tracer une droite (d’) parallèle à (d). Dans le cercle, il suffit de construire les points M’ et N’ diamétralement opposés à M et N, sommets du rectangle MNN’M’.

On a donc, comme ci-dessus, à réaliser le tracé d'une droite, passant par le point P, parallèle aux deux droites (d) et (d’) :

À partir de deux points A et B différents sur (d), tracer deux sécantes (AA’) et (BB’).

Si les droites droites (AB’) et (BA’) sont parallèles, le point P est équidistant de (MN) et (M’N’). La droite (PO) est parallèle à (d) cherchée.

Sinon il est possible de construire le point I d'intersection des droites (AB’) et (BA’). En déduire le point Q et enfin la droite (PQ), parallèle aux deux droites (MN) et (M’N’), est la solution.

Télécharger la figure GéoPlan para_regle.g2w

Perpendiculaire à (d) passant par P

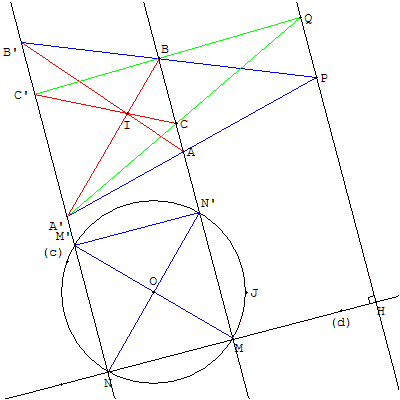
La donnée du cercle (c) permet de tracer deux droites (MN’) et (NM’) perpendiculaires à (d).

D'où le tracé d'une droite, passant par le point P, parallèle aux deux droites (MN’) et (NM’) :

À partir de deux points A et B différents sur (d), tracer deux sécantes (AA’) et (BB’).

Si les droites droites (AB’) et (BA’) sont parallèles, la droite (PO) est la perpendiculaire à (d).

Sinon construire le point I, le point Q et la droite (PQ), parallèle aux deux droites (MN’) et (NM’).
Cette droite est la solution perpendiculaire à (d).

Télécharger la figure GéoPlan perpen_regle.g2w

WikiPédia : construction du milieu d'un segment

  Voir aussi : trois des 15 problèmes de géométrie de la règle

2.2. Perpendiculaire abaissée d'un point sur une droite

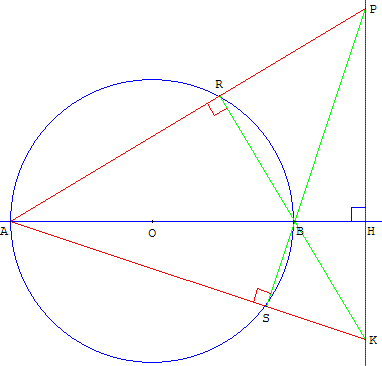
Droite passant par le centre du cercle

2.2.a. Étant donné un cercle de diamètre [AB] et un point P situé ni sur le cercle, ni sur la droite (AB), tracer, uniquement avec une règle non graduée, la perpendiculaire à (AB) issue de P.

Solution

Les droites (PA) et (PB) recoupent le cercle en R et S.
Les droites (AS) et (BR) se coupent en K.
La droite (PK) perpendiculaire à (AB) a été construite uniquement à la règle.

Démonstration

Les triangles ARB et ASB, inscrits dans les demi-cercles de diamètre [AB], sont rectangles et les angles ARK et ASP sont droits.
Le point B, intersection de deux hauteurs (KR) et (PS), est l'orthocentre du triangle APK.
Le côté (PK) est perpendiculaire à la droite (AB), troisième hauteur issue de A.

Télécharger la figure GéoPlan perpen_abaissee.g2w

Image expotée dans WikPédia : construction à la règle seule

2.2.b. Point P situé sur le cercle

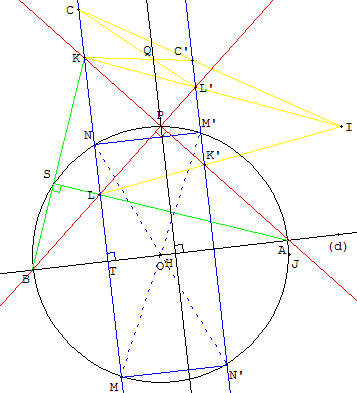
Si le point P est situé sur le cercle, il est confondu avec R et S, ce qui ne permet pas de réaliser la construction précédente, à partir du point P.

Mais à partir d'un point K situé sur la droite (AP), distinct de P, comme ci-dessus construire une perpendiculaire intermédiaire (KL), troisième hauteur du triangle ABK d'orthocentre L. Cette perpendiculaire coupe le cercle en M et N et compléter le rectangle MNM’N’.

Si le point P est équidistant de (MN) et (M’N’) la droite (PO) est perpendiculaire à (d),
sinon (AP) et (BP) coupent (M’N’) en K’ et L’ ; le point I, intersection de (KL’) et de (LK’), permet de construire à la règle le point Q ;
la droite (PQ), parallèle aux deux droites (MN) et (M’N’), est perpendiculaire à (d).

Télécharger la figure GéoPlan perpen_regle_2.g2w

2.2.c. Repère orthonormé

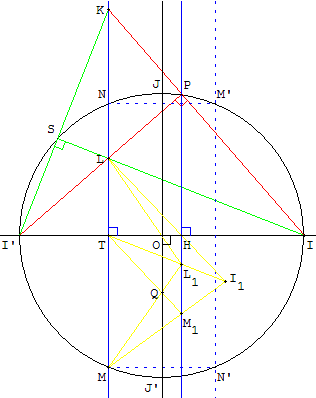
Si (d) est le diamètre [II’] du cercle (c), pour construire la perpendiculaire à (d) élevée du centre O, placer un point P sur le cercle, distinct du milieu du demi-cercle II’.
Comme ci-contre, à partir d'un point K situé sur la droite (AP), construire deux droites intermédiaires (KL) et (PH), perpendiculaires à (d).

À partir des deux droites parallèles (KL) et (PH), il est possible de trouver le point I₁ intersection de (LH) et de (TL₁) permet de construire à la règle le point Q ; la droite (OQ), parallèle aux deux droites (MN) et (PH), est perpendiculaire à (d).

Cette construction fournit le point J de (c) et un repère orthonormé (O, I, J) du plan.

Télécharger la figure GéoPlan repere_regle.g2w

Voir aussi la méthode de K. Von Staudt : équation du second degré
Construire une droite passant par un point de concours situé hors de la feuille : intersection inaccessible

WikiPédia : construction à la règle seule

Liens vers d'autres pages du site

Construction au compas seul

Constructions à l'équerre

Tiers d'un segment

Constructions à la règle à deux bords parallèles seule

Le point de concours de deux droites étant situé hors de la feuille, construire une droite passant par cette intersection inaccessible

Construction, à la règle et l'équerre, d'une perpendiculaire ou d'un carré passant par un point inaccessible

Construction à la règle seule de la polaire d'une droite et de divisions harmoniques

Table des matières

Mobile friendly