Descartes et les Mathématiques
Problèmes d'antan
Sommaire
5. Coniques comme lieux de points
7. Arcs contenus dans un arc capable comme lieux de points
Mobile friendly
Dans d'autres pages du site
L'APMEP et « Descartes et les Mathématiques »
Jeux APMEP : Les tuiles voisines
Problèmes d'antan : rubrique du bulletin de l'APMEP où Michel Fréchet propose d'anciens problèmes à résoudre avec les notions utilisées dans les programmes de l'époque et aussi en se référant aux programmes actuels.
Dans cette page, nous nous contenterons de la preuve par GéoPlan !
5. Problèmes d'antan no 5
Bulletin APMEP no 481 – Mars-avril 2009
Extrait du baccalauréat 1926 de Caen.
Dans un plan, on donne une droite (D) et, sur cette droite
trois points distincts A, B, et C. Par A, B respectivement,
on mène les tangentes (AP) et (BP) (distinctes de (D))
à une circonférence tangente à (D) en C.
Lieu du point d'intersection P de ces deux droites lorsque
la circonférence varie, A, B et C restent fixes.
(On distinguera deux cas :
C est entre A et B ;
C n'est pas entre A et B.)
Solution : bulletin no 484 – Septembre-octobre 2009
Commandes GéoPlan pour le lieu géométrique :
Déplacer le point O.
Touche T : garder la Trace du point P,
touche S : Sortie du mode trace.
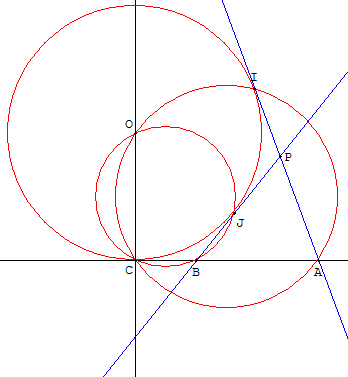
Solution : C n'est pas entre A et B
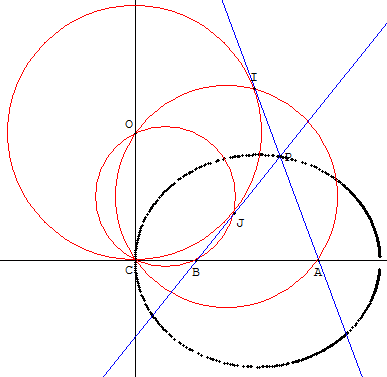
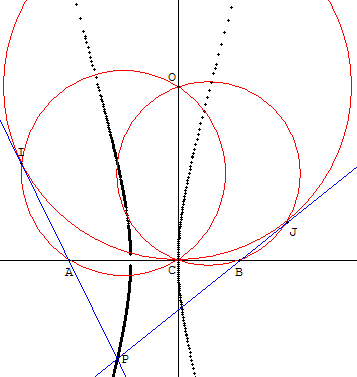
C entre A et B
Télécharger la figure GéoPlan antan5.g2w
7. Problèmes d'antan no 7
Bulletin APMEP no 487 – Mars-avril 2010
Première question du baccalauréat 1926 à Aix-Marseille.
On considère dans un plan un triangle ABC dont les sommets B et C restent fixes ; le sommet A est variable, l'angle A du triangle conservant une valeur constante donnée. On désigne par I1 et I2 les centres des cercles exinscrits au triangle dans les angles B et C.
Calculer en fonction de l'angle A les angles BI1C et BI2C ; déterminer le lieu géométrique des points I1 et I2 quand le sommet A se déplace en restant du même côté de BC.
Figure
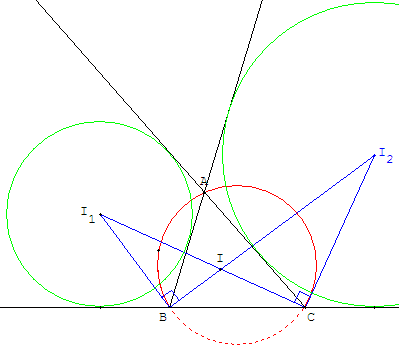
Solution
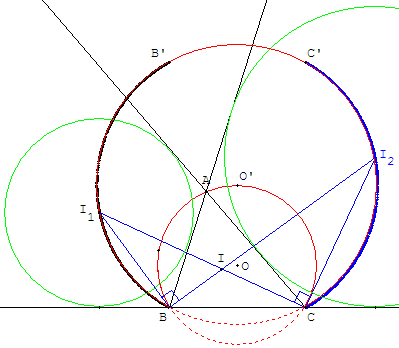
Par un calcul des angles des triangles BI1C et BI2C, on trouve que si α est la mesure l'angle A, les angles BI1C et BI2C mesurent α/2.
Le point A varie sur arc capable d'où l'on « voit » le segment [BC] d'un angle α, arc intersection du cercle (c), circonscrit à ABC, avec un des demi-plans limité par (BC).
Dans le triangle ABC soit les angles ABC = β et ACB = γ avec la somme des angles α + β + γ = π.
Par exemple, pour le triangle BI1C, comme I1 est sur la bissectrice intérieure de l'angle ACB, l'angle BI1C = γ/2.
Le centre I1 est aussi sur la bissectrice extérieure de l'angle ABC, perpendiculaire à la bissectrice intérieure (BI2),
l'angle I1BC = π/2 + β/2.
Donc BI1C = π - I1BC - BI1C = π - (π/2 + β/2) - γ/2 = (π - β - γ)/2 = α/2.
Le lieu géométrique des points I1 et I2 est contenu dans l'arc capable qui « voit » le segment [BC] sous un angle α/2.
Comme l'angle au centre BO’C = α, le centre O’ du cercle (c’), contenant cet arc capable, est situé sur le cercle circonscrit au triangle ABC (et sur la médiatrice de [BC]).
Lorsque l'on déplace A de B en C, le point I1 varie sur l'arc BB’ du cercle (c’) ou B’ est le deuxième d'intersection du cercle avec la perpendiculaire en B à (BC) ; le point I2 varie sur l'arc C’C du cercle (c’) ou C’ est le deuxième d'intersection du cercle avec la perpendiculaire en C à (BC).
Télécharger la figure GéoPlan antan7.g2w
Triangle de Bevan
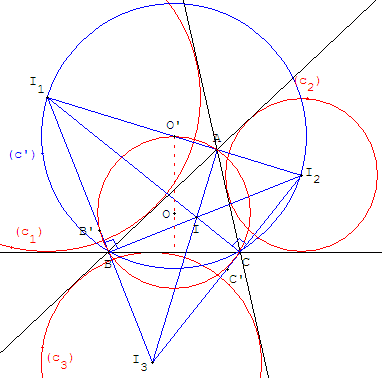
Le cercle (c’) est le cercle de diamètre [I1I2].
Le triangle I1I2I3, formé par les bissectrices extérieures, ayant pour sommet les centres des trois cercles exinscrits, s'appelle le triangle de Bevan du triangle ABC.
Les milieux O’, B’ et C’ des côtés du triangle de Bevan I1I2I3 sont situés sur le cercle circonscrit à ABC.
Figure interactive dans GeoGebraTube : point de Bevan
Page no 155, créée le 26/3/2010