
 Descartes et les Mathématiques
Descartes et les Mathématiques
Exercices de-ci, de-là
Pour chercher et approfondir : diverses constructions, en classe de seconde.
Sommaire
451-2. Diviser l'aire d'un trapèze en deux, en quatre.
Diviser l'aire d'un trapèze en quatre parties égales
486-3. Un cercle comme lieu d'un point
5. Découper deux segments égaux
6. Défi collège
Voir aussi dans d'autres pages du site
452-4. Construction de-ci, de-là : triangles en seconde
453-4. Découpage d'aires dans un carré
462-3. Tangentes aux points de contact : homothétie
478-2. Trouver le lieu géométrique des centres de triangles équilatéraux, inscrits dans un carré : triangle inscrit dans un carré
486-1. Construction sous contrainte : plus court chemin
487-4. Calculs d'aires : triangle équilatéral inscrit dans un rectangle
Rubrique du bulletin de l'APMEP diffusant des exercices proposables à nos élèves, exercices d'origines diverses.
Rubrique crée en 2004 par Serge Parpay et son équipe de Poitevins « Le groupe du Clain » par référence à
une publication, appréciée, de l'IREM de Poitiers lors des années 70 (le Clain est l'affluent de la Vienne qui passe à Poitiers) et un clin œil, aussi, au grand Félix Klein.
Bruno Alaplantive prend le relai en 2009.
451-2. Diviser l'aire d'un trapèze
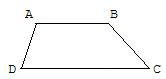
Diviser un trapèze en deux parties d'aires équivalentes par une parallèle aux bases.
Enseignement secondaire spécial et baccalauréat ès sciences
Géométrie théorique et pratique. Eysseric et Pascal. Delagrave 1874
Bulletin APMEP no 451 - mars 2004
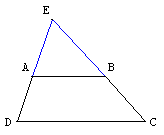
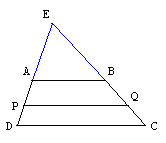
Solution de Bruno Alaplantive : Bulletin APMEP no 453 - septembre 2004
En posant EA = 1 et ED = k = ![]() , pour les aires on a Aire(EDC) = k2Aire(EAB) donc Aire(ABCD)
= (k2 - 1) Aire(EAB).
, pour les aires on a Aire(EDC) = k2Aire(EAB) donc Aire(ABCD)
= (k2 - 1) Aire(EAB).
On obtient, de même, en posant EP = p, Aire(ABQP) = (p2 - 1) Aire(EAB) et la demande Aire(ABQP)
= ![]() Aire(ABCD) équivaut à :
Aire(ABCD) équivaut à :
p2 - 1 = ![]() , soit p = PQ/AB =
, soit p = PQ/AB = ![]() .
.
Partage en deux d'un trapèze : mesure de la base commune
Les côtés parallèles d'un champ en forme de trapèze dont mesurent respectivement 70 m et 230 m.
Si on le partage en deux parties d'aires égales, on peut calculer la longueur du côté de séparation : il mesure 170 m.
Calcul
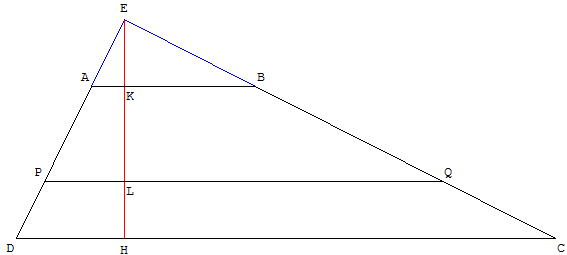
On prolonge les côtés obliques du trapèze jusqu'à ce qu'ils se rencontrent en E.
De façon analogue à la méthode ci-dessus,
en appelant k = ![]() = 230/70,
= 230/70,
on calcule (k2+1)/2 = 289/49,
le rapport p = PQ/AB = ![]() est égal à 170/70, donc PQ = 170 m.
est égal à 170/70, donc PQ = 170 m.
Solution du monde 2
On appelle x la longueur inconnue PQ du muret, h la hauteur EH du grand triangle DCE d'aire 230h, k la hauteur EK du petit triangle ABE d'aire 70k, et l la hauteur EL du triangle PQE d'aire lx.
Ces trois triangles de sommet S sont semblables, d'où la proportionnalité k/70 = l/x = h/230 d'où k = 70h/230 et l = hx/230.
lx -70k aire du trapèze ABQP est égal à 230h - lx aire du trapèze PQCD, soit 2lx = 70k + 230h.
En substituant k et l, on établit l'équation suivante :
x2h/230 = ![]() (702h/230 + 230h) qui se simplifie par h/230 en x2 =
(702h/230 + 230h) qui se simplifie par h/230 en x2 = ![]() (702 + 2302).
(702 + 2302).
Il vient x = 170.
![]() Télécharger la figure GéoPlan mon_606.g2w
Télécharger la figure GéoPlan mon_606.g2w
Construction à la façon de Descartes
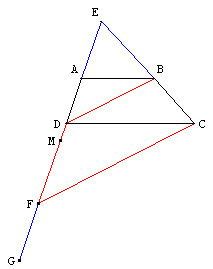
La parallèle à (BD) coupe (ED) en F. Les triangles EDB et EFC sont semblables avec le rapport de similitude k.
Comme ED = k, on a EF = k2.
En reportant l'unité EA en FG, puis en plaçant le milieu M de [EG], on a EM = ![]() .
.
On termine alors par la construction classique de la racine carrée d'un nombre :
Reporter l'unité EA en EA’ et tracer le cercle de diamètre [MA’]. La perpendiculaire à (MA’) en E coupe le cercle en H. EH est la moyenne géométrique de EA’ et EM.
Il suffit de rabattre H en P sur [ED] et de terminer (PQ) parallèle aux bases du trapèze.
![]() Télécharger la figure GéoPlan ex2_451.g2w
Télécharger la figure GéoPlan ex2_451.g2w
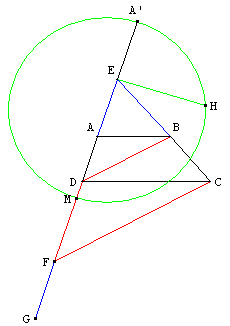
![Rabattre H en P sur [ED] et de terminer (PQ) construction a la facon de descartes du partage de l'aire d'un trapeze - copyright Patrice Debart 2010](exercice_de_ci_de_la/trapeze5.gif)
Diviser un trapèze en quatre parties égales
Question du Forum Futura Sciences Generation
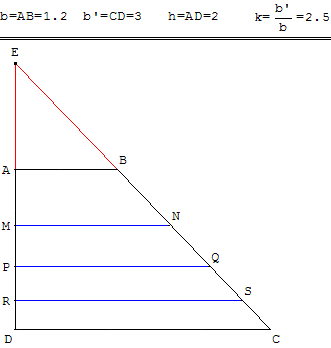
Diviser en 4 parts égales l'aire d'un trapèze rectangle.
Ces 4 parts ont leurs bases parallèles à la base du grand trapèze, cela revient à diviser ce grand trapèze en 4 petits trapèzes de même aire…
ABCD est un trapèze rectangle en D, de petite base b = AB, de grande base b’ = CD
et de hauteur h = AD.
Les côtés non parallèles du trapèze se rencontrent en E.
La propriété de Thalès dans le triangle ECD permet d'écrire les rapports :
k = ![]() =
= ![]() =
= ![]() , or
, or ![]() =
= ![]() = 1 +
= 1 + ![]() , soit
, soit ![]() = k - 1 et EA =
= k - 1 et EA = ![]() =
= ![]() .
.
Le partage en quatre se fait par les segments [MN], [PQ] et [RS] parallèles aux bases.
[PQ] partage en deux, cas traité ci-dessus avec EP = p EA :
Aire(ABQP) = (p2 - 1) Aire(EAB) et la demande Aire(ABQP) = ![]() Aire(ABCD) équivaut à :
Aire(ABCD) équivaut à :
p2 - 1 = ![]() (k2 - 1), soit p =
(k2 - 1), soit p = ![]() .
.
[MN] partage au quart l'aire du trapèze avec EM = m EA :
Aire(ABNM) = (m2 - 1) Aire(EAB) et Aire(ABNM) = ![]() Aire(ABCD) équivaut à :
Aire(ABCD) équivaut à :
m2 - 1 = ![]() (k2 - 1), soit m =
(k2 - 1), soit m = ![]() .
.
[RS] partage aux trois quarts l'aire avec ER = r EA :
Aire(ABSR) = (r2 - 1) Aire(EAB) et Aire(ABSR) = ![]() Aire(ABCD) équivaut à : r2 - 1 =
Aire(ABCD) équivaut à : r2 - 1 = ![]() (k2 - 1), soit r =
(k2 - 1), soit r = ![]() .
.
![]() Télécharger la figure GéoPlan div_trap_en4.g2w
Télécharger la figure GéoPlan div_trap_en4.g2w
486-3. Cercle comme lieu d'un point
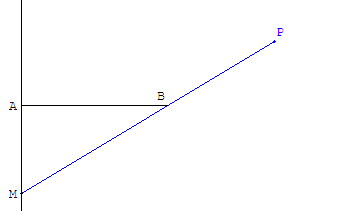
M. Guisnée - Paris
Soit un segment [AB] et (d) sa perpendiculaire en A.
On choisit un point M pris sur (d) et on construit le point P de la demi-droite [MB), n'appartenant pas au segment [MB], qui vérifie :
PB × BM = AB2.
Déterminer le lieu du point P lorsque M varie sur (d).
Commandes GéoPlan pour le lieu géométrique :
Déplacer le point M.
Touche T : garder la Trace du point P,
touche S: Sortie du mode trace.
Taper L pour afficher/effacer le Lieu des points P et les triangles BCP et BCQ.
Solution
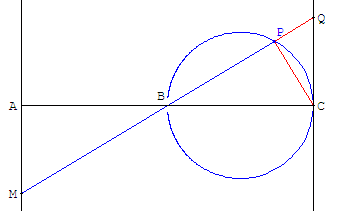
Soit C le point symétrique de A par rapport à B, le point Q symétrique de M et la droite (d’) perpendiculaire en C à (AC).
Le lieu est le cercle de diamètre [BC], privé de B.
Comme BM = BQ, dans le triangle rectangle BCQ on a :
PB × BQ = BC2.
La relation métrique donnant le carré du petit côté BC, montre que le point P est le pied de la hauteur issue de C.
L'angle BPC est droit.
![]() Télécharger la figure GéoPlan ex486-3.g2w
Télécharger la figure GéoPlan ex486-3.g2w
5. Découper deux segments égaux
Un problème original de Serge Parpay créé pour le rallye Mathématique Poitou-Charentes - Corol'aire no 69 - Juin 2007
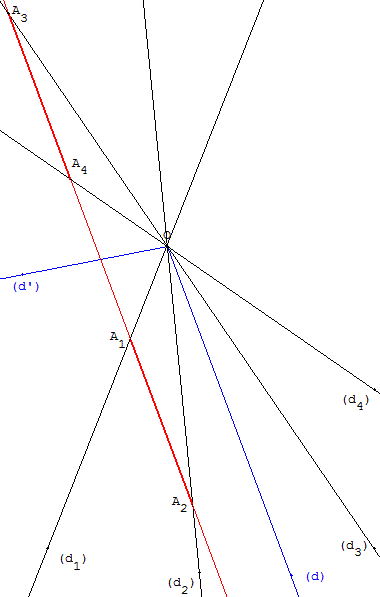
Quatre droites (d1), (d2), (d3), (d4) sont concourantes en un point O.
Construire une droite (Δ) qui coupe ces quatre droites respectivement en A1, A2, A3, A4 de telle sorte que A1A2 = A3A4.
Analyse
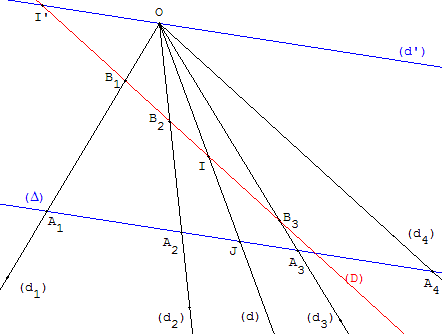
Soit (Δ) une droite répondant à la question (remarquons que toute parallèle à (Δ), ne passant par O, conviendrait également).
A1A2 = A3A4, les segments [A1A4] et [A2A3] ont même milieu J. Soit (d) la droite passant par O et J et (d’) la parallèle à (Δ) passant par O.
J étant le milieu de [A1A4] les droites (d1, d4, d, d’) forment un faisceau harmonique.
Réciproquement, soit (D) une droite parallèle à (d4) coupant les trois autres rayons du faisceau en B1, I et I’ ; le point B1 est alors le milieu de [II’].
Par ailleurs, comme J est aussi le milieu de [A2A3], les droites (d2, d3, d, d’) forment un autre faisceau harmonique. (B2, B3, I, I’) est une division harmonique.
Avec le milieu B1 de [II’] la relation de Newton permet d'écrire :
B1I2 = B1I’2 = B1B2 × B1B3.
Cette relation va permettre la construction de I et I’ et, par suite, des droites (d) et (d’).
![]() Télécharger la figure GéoPlan deux_segment1.g2w
Télécharger la figure GéoPlan deux_segment1.g2w
Construction des points I et I’
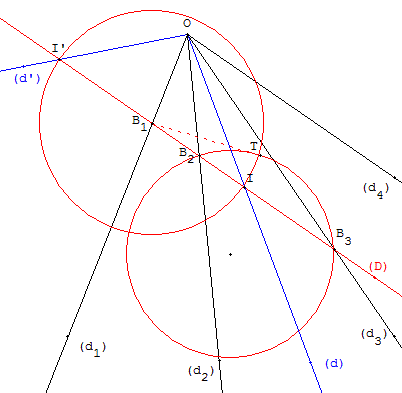
Une droite (D) parallèle à (d4) donne les points B1, B2, B3.
Le produit B1B2 × B1B3 est la puissance du point B1 par rapport à un cercle passant par B2 et B3.
On trace alors un tel cercle et une tangente (B1T)) à ce cercle.
Le cercle de centre B1 passant par T coupe la droite (D) en I et I’.
On a bien B1T2 = B1B2 × B1B3 = B1I2 = B1I’2.
En joignant O à I et I’, on construit les droites (d) et (d’) cherchées.
![]() Télécharger la figure GéoPlan deux_segment2.g2w
Télécharger la figure GéoPlan deux_segment2.g2w
Une solution
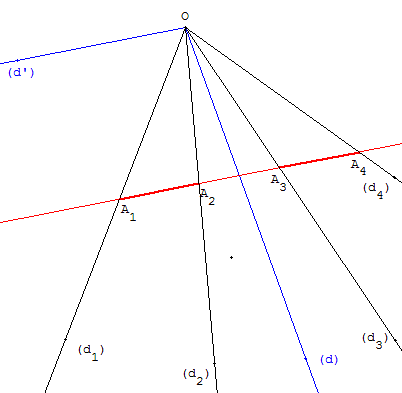
En menant, à partir d'un point A1 situé sur (d1), une droite (Δ) parallèle à (d’), on trouve une solution au problème.
De même ci-contre, une parallèle (Δ) à (d) donne une autre solution du problème.
![]() Télécharger la figure GéoPlan deux_segment3.g2w
Télécharger la figure GéoPlan deux_segment3.g2w
Une autre solution
![]() Télécharger la figure GéoPlan deux_segment4.g2w
Télécharger la figure GéoPlan deux_segment4.g2w
6. Défi collège
Défi proposé par Serge Parpay
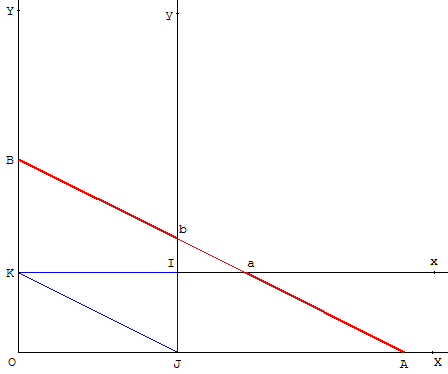
Soit deux angles XÔY et xÎy aux côtés respectivement parallèles.
Construire une droite (D) coupant [OX) en A, [OY) en B, [Ix) en a et [Iy) en b telle que Aa = Bb.
Déplacer les points A ou a pour trouver la solution.
Deux angles droits

![]() Télécharger la figure GéoPlan deux_defi_parpay1.g2w
Télécharger la figure GéoPlan deux_defi_parpay1.g2w
Solution
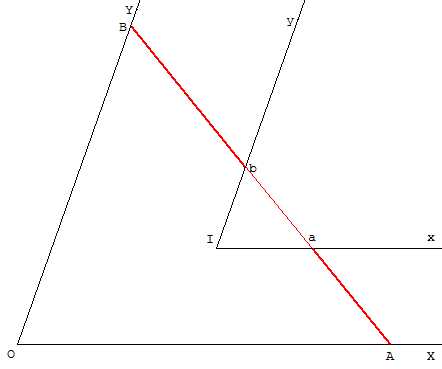
Deux angles aigus
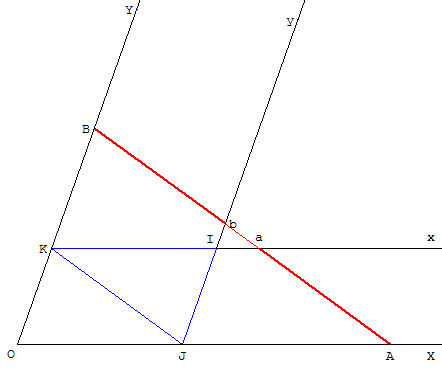
Solution avec deux angles aigus
![]() Télécharger la figure GéoPlan deux_defi_parpay2.g2w
Télécharger la figure GéoPlan deux_defi_parpay2.g2w
Table des matières
Dans d'autres pages du site
L'APMEP et « Descartes et les Mathématiques »
APMEP : Problèmes d'antan
Téléchargement des ancienne versions 2008 :
![]() Télécharger exercices_de_ci_de_la.pdf : ce document « .pdf »
Télécharger exercices_de_ci_de_la.pdf : ce document « .pdf »
Google considère l'URL originale comme une erreur de type "soft 404" mais référence la copie !
Copyright 2004 - © Patrice Debart
![]() Google friendly
Google friendly
Rétrolien (backlink)
Exercices du bulletin vert : Patrice Debart tient quant à lui un site très complet d’activités et exercices en tout genre de la Sixième à la Terminale (!) proposant entre autres des reprises d’exercices de-ci, de-là. À ne pas rater non plus !
Page no 78, réalisée le 16/10/2004
mise à jour le 23/3/2010