Descartes et les Mathématiques

Leçons de géométrie

Capes Externe de Mathématiques 2007 - Épreuve sur dossier
Thème 21 : problème d'incidence : parallélisme et orthogonalité

Par Françoise Bourhis-Lainé

Sommaire

1. Deux carrés autour d'un triangle

2. Section d'un tétraèdre par un plan

3. Cube

1. Deux carrés autour d'un triangle

Exercice

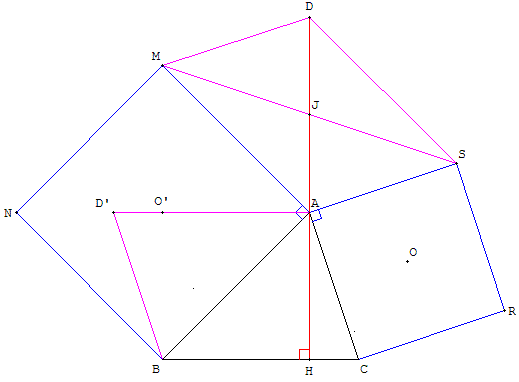
ABC est un triangle quelconque tel que (AB, AC) = α (α ∈ ] 0, 2π[)
On construit extérieurement à ce triangle les carrés (ACRS) et (BAMN) de centres respectifs O et O’ tels que
(AM, AB) = (AC, AS) = π/2(2π)
On construit aussi le parallélogramme (MASD) de centre I.
Montrer que la droite (AD) est une hauteur du triangle (ABC) et que AD = BC.

Travail demandé

Après avoir analysé et résolu ce problème ouvert, le candidat répondra aux questions suivantes :
Question 1 : Analysez l'intérêt de cet énoncé au regard des exigences du programme
Question 2: Quelles sont les connaissances de géométrie que doit posséder un élève pour résoudre l'exercice ? Proposez un énoncé de manière à rendre ses connaissances disponibles.
Question 3 : Quel peut être l'apport de l'outil « nombres complexes » ? Envisageriez-vous une réécriture de l'énoncé ?
Quel prolongement proposeriez- vous à l'exercice sur le thème parallélisme et orthogonalité ?
Question 4 : Proposer un exercice sur le même thème…

Indications

Classe de seconde - rotation

Dans le carré ACRS on a AC = AS et (AC) est perpendiculaire à (AS) et la rotation R(A, π/2) transforme C en S et vect(AC) en vect(AS).

Dans le parallélogramme (MASD), AS = MD et (AS)//(MD).

La rotation R(A, π/2) transforme D en D’ ; vect(AD) en vect(AD’) et M en B,
donc vect(DM) en vect(D’B).

On a donc DM = D’B et (DN) est perpendiculaire à (D’B).

D'où AC = AS = MD = D’B,
(D’B) et (AC), perpendiculaires à (AS) et (MD), sont parallèles.

ABCD’ est un parlera donc AD’ = BC et (AD’)//(BC),
donc AD = AD’ = BC, soit AD =BC ;
et comme (AD) est perpendiculaire à (AD’) et (AD’)//(BC) on a (AD) est perpendiculaire à (BC).

Classe de première S − produit scalaire

vect(AD) = vect(AS) + vect(AM)

BC = AC−AB

BC.AD = (AS+AM) × (AC−AB) = 0 − AS.AB + AM.AC − 0
    = − bc cos(α+π/2) + bc cos [(π−α)+π/2] = 0 donc (AD) est perpendiculaire à (BC).

Al-Kashi permet de calculer BC² : a² = b² + c² − 2 b c cos(α),
AD² = (AC−AB)² = AC² + AB² − 2 bc cos(AS, AM) et comme cos(AS, AM) = cos(π−α) = cos(α) on a AD² = a² et AD = BC = a.

Question 1

…

Télécharger la figure GéoPlan parallelisme_orthogonalite.g2w

Question 2 : propriétés de la rotation et du parallélogramme

Introduire D’ dans l'énoncé…

Question 3 : TS nombres complexes

L'apport des complexes est la grande simplicité des calculs et la mise en évidence directe de la rotation z’ = iz.

Prendre comme origine A, les affixes des points sont notées par les minuscules correspondantes.

s = ic, m = −ib donc d = i(c−d).

Prolongements sur le thème parallélisme et orthogonalité

(BR) orthogonale à (CD) ou (CN) orthogonale à (BD) ; (BR), (CN) et (AD) concourantes.

voir carrés autour de BOA : droites concourantes,   droites perpendiculaires

DNR, triangle rectangle isocèle
voir carrés autour de BOA : triangle rectangle isocèle

IOO’, triangle rectangle isocèle
voir carrés autour de BOA : autre triangle rectangle isocèle

Le triangle ABC a même que ASM égale à la moitié de l'aire du parallélogramme (MASD).
voir carrés autour de BOA : extriangles

Question 4 : Proposer un exercice sur le même thème

voir problèmes du BOA,   carrés autour de BOA
Thème 21-b problème d'incidence : parallélisme et orthogonalité

2. Section d'un tétraèdre par un plan

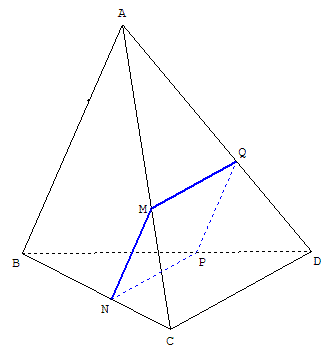
Soit A, B, C, D 4 points non coplanaires.
Un plan P parallèle aux droites (AB) et (CD), ne contenant aucun des sommets, coupe les arêtes du tétraèdre [AC], [BC], [BD], [AD] respectivement en M, N, P, Q (voir figure ci-dessous).
1) Montrer que le quadrilatère MNPQ est un parallélogramme.
2) Supposons que AB = 4 CD.
Peut-on choisir le plan P de telle manière que MNPQ soit un losange ?

Travail demandé

Après avoir résolu et analysé l'exercice, le candidat rédigera sur sa fiche les réponses aux questions suivantes :
Question 1 : Indiquer le niveau où pourrait être donné l'exercice. Analyser son intérêt au regard des exigences du programme.
Question 2 : Énoncer les théorèmes mis en jeu dans l'exercice.
Question 3 : Que penser de l'hypothèse relative aux longueurs respectives des côtés du tétraèdre (cf 2) ?
Question 4 : Proposer un exercice sur le même thème…

Indications

Question 1 : seconde-première

Question 2 : théorème du toit

Question 3: Thalès

M est le point de [CA] situé au 1/5 à partir de C.
Plus généralement,
si AB = k CD alors
MC = k MA et CM = CA/(k+1).

Voir réciproque parallélogramme comme section plane d'un tétraèdre

Figure 3D dans GeoGebraTube : parallélogramme dans un tétraèdre

3. Cube

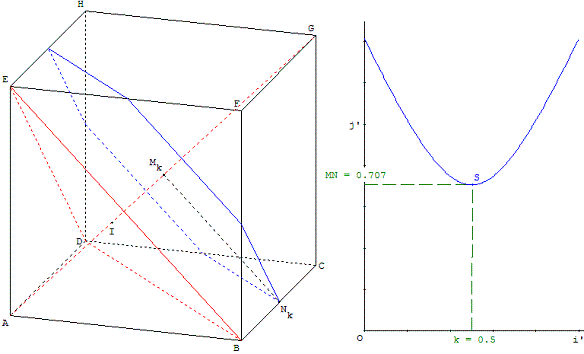
Un exercice menant à un problème d'optimisation :
deux cadres dans l'écran ; le cadre de gauche pour la figure géométrique, le cadre de droite pour une fonction permettant la recherche d'extrema.

Représenter un cube ABCDEFGH d'arête 1.

L'espace est rapporté au repère orthonormal (A ; , , ).

A) UN TRIANGLE ET SON CENTRE DE GRAVITÉ

• Démontrer que le triangle BDE est équilatéral.
• Soit I le centre de gravité du triangle BDE.
• Calculer les coordonnées de I.

Démontrer que =  ; que peut-on en déduire pour les points A, I, G ?

• Prouver que I est le projeté orthogonal de A sur le plan (BDE).

B) UNE DROITE PARTICULIÈRE

Pour tout nombre k, on définit deux points M_k et N_k, ainsi qu'un plan P_k de la façon suivante :

M_k est le point de la droite (AG) tel que _k = k ;

P_k est le plan passant par M_k et parallèle au plan (BDE) ;

N_k est le point d'intersection du plan P_k et de la droite (BC).

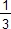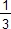• Identifier P, M, N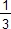 en utilisant les points déjà définis ;

Calculer la distance MN .

• Calcul des coordonnées de N_k

a) Calcul des coordonnées de M_k dans le repère (A ; , , ).

b) Déterminer une équation du plan P_k dans ce repère.

c) En déduire que le point N_k a pour coordonnées (1, 3k−1, 0)

3) Pour quelles valeurs de k la droite (M_kN_k) est-elle orthogonale à la fois aux droites (AG) et (BC) ?

4) Pour quelles valeurs de k la distance M_kN_k est-elle minimale ?

5) Tracer sur la figure la section du cube par le plan P.

Tracer la droite (MN) sur la même figure.

Travail demandé au candidat

Après avoir résolu et analysé l'exercice, le candidat rédigera sur sa fiche les réponses aux questions suivantes

1) Dégager les outils et les connaissances mis en jeu dans la résolution de cet exercice.
2) Dans quelle classe peut-il être proposé ? A quel stade de l'apprentissage ?
3) Proposer une autre démonstration de la troisième question de la partie A.
4) Proposer un exercice sur le même thème.

Recherche d'extrema dans le cube

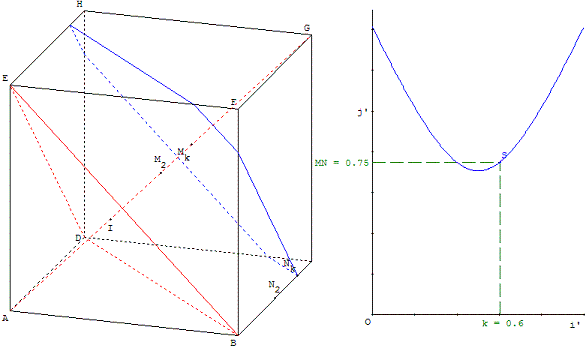
Cliquer dans la figure et déplacer le point M avec la souris ou les flèches du clavier.
Touche T : Tracé point par point du graphe,
touche S pour Sortir du mode trace,
touche L : dessin en bloc du graphe.

Télécharger la figure GéoSpace cube_plan.g3w

Extrema dans le cube

Table de matières

Dans d'autres pages du site

La géométrie au CAPES

Problèmes de géométrie

Carrés autour de BOA

GeoGebra 3D: Sections de cube

Mobile friendly

Capes, page n^o 4, créée le 02/5/2007