Descartes et les Mathématiques
La géométrie dans l'espace en terminale S
Épreuve pratique 2009 supprimée
Mathématique avec GéoSpace en TS - Sujets 2009 de géométrie de l'épreuve pratique.
Sommaire
Sujets retenus
31. Lieu géométrique de points dans l'espace
Sujet non retenu
33. Section plane d'un tétraèdre et optimisation d'une distance
Sujets retenus en 2009
31. Lieu géométrique de points dans l'espace
Situation
Le but de l'exercice est de déterminer le lieu d'un point défini comme barycentre, à coefficients positifs, de certains sommets d'un cube donné.
Énoncé
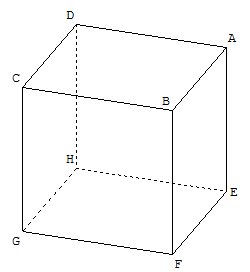
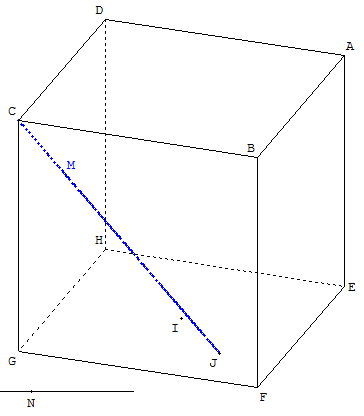
Dans l'espace muni d'un repère orthonormal R, on considère le cube ABCDEFGH reproduit ci-contre.
On note I le centre de la face EFGH et J le milieu du segment [IF].
Pour tout réel m de l'intervalle [0; 1], on note M le barycentre des points pondérés suivants :
(E ; m), (F ; 2m), (G ; m), (C ; 4 - 4m).
Le but de l'exercice est la recherche du lieu du point M lorsque m décrit l'intervalle [0 ; 1].
1. (a) À l'aide d'un logiciel de géométrie dans l'espace, construire le cube ABCDEFGH ainsi que les points I et J.
(b) Construire le point M barycentre du système de points pondérés (E ; m), (F ; 2m), (G ; m),
(C ; 4 - 4m) pour m ∈ [0 ; 1].
(c) Émettre une conjecture quant au lieu du point M lorsque m décrit l'intervalle [0 ; 1].
2. (a) Démontrer que les points M, F, I et C sont coplanaires.
(b) Déterminer une relation entre les vecteurs 
et 
.
(c) Conclure alors quant au lieu du point M lorsque m décrit l'intervalle [0 ; 1].
Figures 3D dans GeoGebra Tube : cube, cube en fil de fer
Production demandée
- Construction de la figure à l'aide d'un logiciel de géométrie dynamique.
- Énoncé de la conjecture.
- Relation et démonstrations demandées dans la question 2.
Indications
D'après la fonction vectorielle de Leibniz pour tout point O on a :
m 
+ 2m 
+ m 
+ (4 - 4m) 
= (m + 2m + m + (4 - 4m)) 
,
soit m ( + 2 + ) + (4 - 4m) = 4 .
2. (a) I est le milieu de [EG] donc + = 2 
et m (2 + 2 ) + (4 - 4m) = 4 .
Soit M le barycentre des points pondérés (I ; 2m), (F ; 2m),
(C ; 4 - 4m).
Le point M appartient au plan (FIC) formé par ces trois points.
(b) J le milieu du segment [IF], d'où 2 + 2 = 4 
;
d'où 4m + (4 - 4m) = 4 .
Par associativité, le point M est le barycentre du système de deux points pondérés
(J ; m), (C ; 1 - m).
En plaçant O en C on a : = m .
Remarque :
le point J est le barycentre du système de points pondérés (E ; 1), (F ; 2), (G ; 1).
(c) Le point M décrit le segment [CJ]. = m , lorsque m parcourt [0, 1] tous les points du segment sont atteints.
Télécharger la figure GéoSpace cube_lieu.g3w
Remarques : Dans ce problème, la géométrie dynamique se borne à taper la liste
(E ; m), (F ; 2m), (G ; m),
(C ; 4 - 4m) dans GéoSpace. Le rôle des points E et G est léger. L'espace n'est justifié que par la question 2.(a) un peu poussive. Dès que l'on utilise le point I, on obtient un problème plan sans grand intérêt.
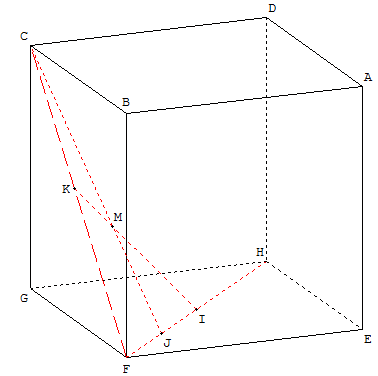
Il aurait été bien plus intéressant d'en faire un problème d'incidence en plaçant le barycentre partiel K de (F ; 2m), (C ; 4 - 4m), puis en définissant M comme point d'intersection des droites (CJ) et (KI). Enfin de faire retrouver les coordonnées barycentriques de M dans le cube en considérant ces deux droites dans le triangle FIC, pour terminer par les questions 2. (b) et 2. (c).
Télécharger la figure GéoSpace cube_lieu2.g3w
Compétences évaluées
Compétences TICE
- Construire une figure à l'aide d'un logiciel de géométrie dans l'espace ;
- Conjecturer un lieu de points.
Compétences mathématiques
- Démontrer que des points sont coplanaires ;
- Utiliser la géométrie vectorielle.
75. Volume d'un tétraèdre, construit sur un cube
Situation
On considère un cube de l'espace, formé par ses sommets ABCDEFGH (voir figure ci-contre). Sur la demi-droite [AE) on considère un point variable K.
Le but de l'exercice est de rechercher une position du point K, pour laquelle le volume du tétraèdre BDGK est égal à la moitié du volume du cube.
Énoncé
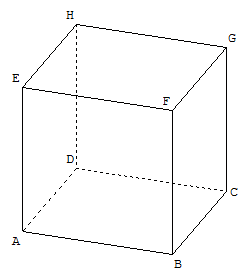
1. À l'aide d'un logiciel, représenter un cube ABCDEFGH.
Placer un point K variable sur la demi-droite [AE).
2. Pour quelle position du point K le volume du tétraèdre BDGK semble-t-il être égal à la moitié de celui du cube ?
Appeler l'examinateur pour une vérification de la position du point K trouvée.
3. En supposant que K occupe la position trouvée à la question 2., conjecturer la nature des triangles KGB et KDG à l'aide du logiciel.
4. Démontrer que lorsque le point K occupe la position trouvée à la question 2., le volume du tétraèdre BDGK est bien la moitié du volume du cube.
Production demandée
- Affichage des valeurs numériques nécessaires pour émettre la conjecture de la question 2.
- Éléments de preuve pour la question 4.
Indications
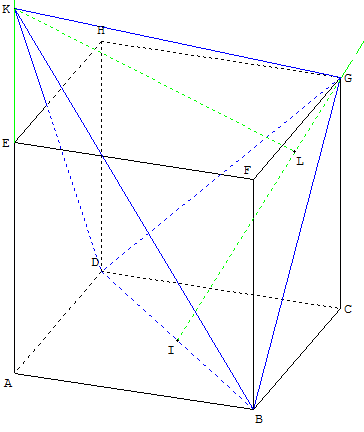
Le volume du tétraèdre BDGK semble être égal à la moitié de celui du cube lorsque le point est K situé a une distance de A égale au double du côté du carré.
Les triangles KGB et KDG sont alors rectangles.
Avec GéoSpace, il n'est pas possible d'afficher directement des volumes ou des angles.
Créer des variables numériques : y égale au volume du Tétraèdre et g égale à l'angle BGD, et les afficher.
Déplacer le point K, visualiser y et émettre la conjecture.
Il est possible de tracer la droite passant par K perpendiculaire au plan (BDG).
Cette droite coupe le plan en L et [KL] est la hauteur du tétraèdre qui rencontre le plan de base sur la demi-droite [IG) médiatrice du triangle équilatéral BDG.
Technique GéoSpace
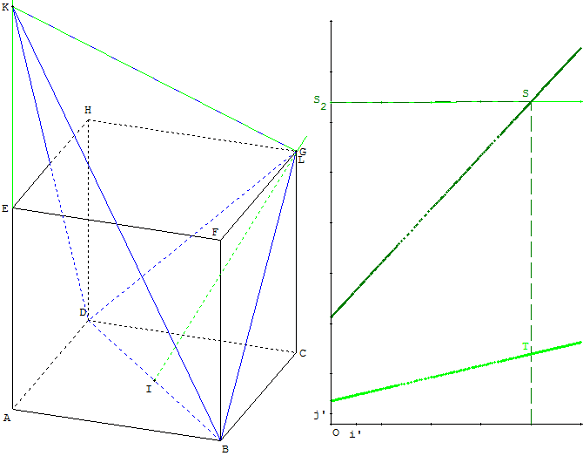
Avec les menus de GéoSpace, on ne peut pas calculer la longueur d'un segment, mais taper directement dans le texte de la figure :
x = AK z = KL
Dans un repère (O, i’, j’) afficher les points S(x, y) et T(x, z).
Se placer en mode trace et déplacer le point K, taper S pour trouver la solution.
Télécharger la figure GéoSpace volume_tetra.g3w
(4) En visualisant le graphique ci-dessus, on réalise que le volume est une fonction linéaire de x, donc un problème du premier degré résoluble en seconde.
Le volume du tétraèdre est donné par la formule V = 
SBDG × KL.
Si c est le côté du carré, le côté du triangle équilatéral, une diagonale du carré, est égal à a = EG = c 
.
L'aire du triangle équilatéral est SBDG = 
a2 = 
c2.
Pour le calcul de la hauteur KL, placer le plan AEG de face (touche F avec GéoSpace).
JEG est un triangle rectangle de petits côtés JE = 2c et EG = a = c ,
l'hypoténuse est JG = c 
.
Dans ce triangle rectangle sin(EJG) = EG/JG = 
.
Dans le triangle rectangle semblable JKL, on a : KL = JK sin(EJG) = JK .
Donc KL = (x + c) .
D'où V = SBDG × KL = c2 × (x + c) = 
c2 × (x + c).
Le volume V est 
c3 si x = 2c.
Pour l'épreuve pratique, après le calcul de SBDG, il n'était demandé que de vérifier, lorsque x = 2c,
que KL = c , d'où V = c2 × c = c3.
Télécharger la figure GéoSpace volume_tetra2.g3w
Remarque perfide : bel exercice qui justifie la géométrie dynamique, mais gâché par une dernière question sans ampleur.
Avant ma retraite, je faisais ce genre de calcul en seconde, maintenant on ne propose plus qu'une vérification en terminale S, bientôt géométrie et calcul seront délocalisés en Chine ou en Inde.
Compétences évaluées
Compétences TICE
- Réaliser des constructions avec un logiciel de géométrie dans l'espace ;
- Émettre et tester des conjectures.
Compétences mathématiques
- Calculs de longueurs, d'aires et de volumes ;
- Orthogonalité dans l'espace.
Technique GéoSpace : une seule figure avec deux zones
Dans l'exemple ci-dessus, je préfère utiliser une seule figure avec deux zones : une zone pour visualiser une situation géométrique, l'autre pour tracer une fonction dans un repère (O, i’, j’).
Sujets de 2009 non retenus
33. Section plane d'un tétraèdre et optimisation d'une distance
Situation
On donne un tétraèdre dans l'espace muni d'un repère orthonormal. Il s'agit de minimiser la distance entre deux points définis à partir des sommets du tétraèdre.
Énoncé
Dans l'espace rapporté à un repère orthonormal (O ; 
, 
, 
), on définit les points A(l, 0, 0), B(0, 1, 0) et C(0, 0, 1) et le point I milieu du segment [AB].
Partie expérimentale.
1. (a) À l'aide d'un logiciel de géométrie dans l'espace, représenter le tétraèdre OABC et le point I.
(b) Pour un point M du segment [AC], on définit le plan P passant par le point I et orthogonal à la droite (IM). Tracer la section du tétraèdre OABC par le plan P.
(c) Le plan P coupe la droite (OB) en un point N. Construire le point N et tracer le segment [MN].
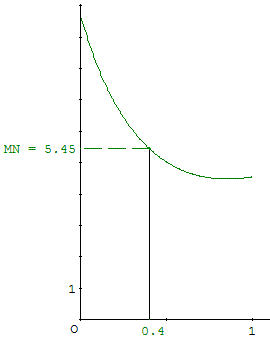
2. Étudier à l'aide du logiciel, les variations de la longueur MN et conjecturer la position du point M, sur le segment [AC], telle que cette longueur soit minimale. Quelle est, d'après le logiciel, cette longueur minimale ?
Démonstration
On définit le réel t = AC et on admet que les coordonnées des points M et N sont respectivement M(1−t, 0, t) et N(0, t, 0) (cf. l'équation paramétrique de AC).
1. Calculer la longueur MN en fonction de t.
2. Déterminer la valeur de t pour laquelle cette longueur est minimale.
Autre exercice
Dans l'espace, on donne un tétraèdre OABC et le milieu I de [AB]. Soit M un point quelconque du segment [AC]. Le plan passant par I et orthogonal à la droite (IM) coupe la droite (OB) en N. On cherche à minimiser la distance MN.
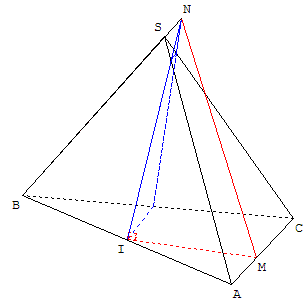
Télécharger la figure GéoSpace section_tetraedre.g3w, la figure GéoSpace tetraedre_fct.g3w
Technique GéoSpace : communication entre deux figures - importation active
Avec les menus de GéoSpace, on ne peut pas calculer la longueur d'un segment, mais taper directement dans le texte de la figure :
y = MN
La figure de gauche, section_tetraedre, importe(Menu >Piloter>Importer) la valeur de x, de la figure de droite. x doit être défini comme réel non borné dans cette figure, bien qu'il soit borné entre 0 et 1 dans tetraedre_fct (pour permettre d'afficher la courbe comme lieu de points).
Dans tetraedre_fct le tétraèdre et sa section sont dupliqués, en mode non dessiné, pour réaliser le calcul de y.
Pour obtenir un axe (Ox) horizontal, le graphe est réalisé avec le plan (Oxz) de face correspondant à l'instruction :
Rotations de Rxyz: verticale: 90 horizontale: 0 frontale: 0
Compétences évaluées
Compétences TICE
• Constructions géométriques et mesures avec un logiciel de géométrie dynamique.
Compétences mathématiques
• En géométrie analytique, calcul de la distance de deux points de l'espace ;
• Recherche d'un extremum d'une fonction.
Table des matières
Sujets retenus
31. Lieu géométrique de points dans l'espace
Sujet non retenu
33. Section plane d'un tétraèdre et optimisation d'une distance
Épreuve pratique en TS
Géométrie dans l'espace
Géométrie plane
Mobile friendly
|
|
Page no 146, créée le 25/6/2009 |