Descartes et les Mathématiques

Maxima - Minima dans l'espace

Illustration du passage d'une situation géométrique à une situation d'analyse
en utilisant deux figures qui communiquent entre elles.

Sommaire

1. Mesure maximum d'un angle avec GéoPlan

2. Volume maximal d'un cylindre
    GéoPlan/GéoSpace : Mode d'emploi pour la communication entre figures et l'importation active
3. Parallélépipède dans une pyramide

Fonctions et géométrie dans l'espace

1. Mesure maximum d'un angle

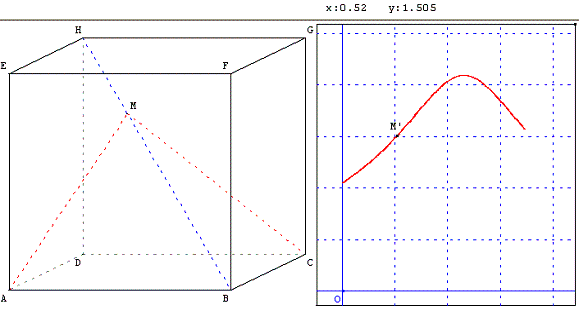
Pour des figures en perspective cavalière, GéoPlan est parfois la solution la plus simple (mais on perd tout l'aspect dynamique) !

Dans le cube ABCDEFGH de côté 1, le point M varie sur la diagonale principale [HB].
Le problème consiste à trouver la position du point M telle que la mesure de l'angle AMC soit maximale.
On appelle x la longueur du segment HM et y la mesure de l'angle AMC. Le point M’ du graphique a pour coordonnées (x, y) (affichées ci-dessous).

L est la courbe représentative de y = f(x) avec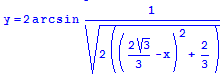

Télécharger la figure GéoPlan max_angle.g2w

2. Communication entre figures - Importation active

Volume maximal d'un cylindre

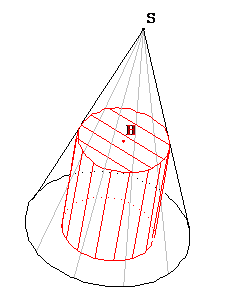
Situation

On cherche le cylindre de volume maximal inscrit dans un cône. Dans la figure Cyl_Cone, un point H est variable sur le segment [oS]. Les variables x et V représentent respectivement la longueur oH et le volume du cylindre.

Utilisation

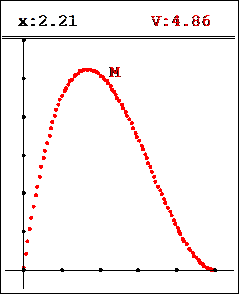
Charger les deux figures (fermer éventuellement toutes les autres) et les placer en mosaéque (menu : Fenêtres). Les valeurs de x et de V (affichées dans graphiq) ne sont pas forcément les mêmes dans les deux figures. Pour actualiser ces valeurs, il faut rendre active la figure Cyl_Cone.g3w. Pour observer la courbe de la fonction telle que V soit l'image de x par cette fonction, il faut mettre la figure graphiq.g3w en mode « Trace ».

Le calcul de V en fonction de x utilise seulement le théorème de Thalès. C'est une fonction polynéme du troisième degré qui peut donc s'étudier en première.

Télécharger la figure GéoSpace Cyl_Cone.g3w ; la figure GéoSpace Graphiq.g3w

Commentaire sur la réalisation

Dans Cyl_Cone, le point H est un point variable sur le segment [oS] et le cylindre est créé en utilisant le point d'intersection du plan passant par H et parallèle au plan de la base du cône avec une génératrice du cône.

Dans graphiq, on définit deux réels libres x et V puis le point M de coordonnées (x, V) dans le plan oxy muni de son repère canonique. La figure est importatrice (article du menu Importer, coché dans le menu Piloter). De plus, on a choisi la vue standard avec oxy de face et on a placé la figure en mode « Plan de face maintenu de face » pour simuler une figure plane.

Modification éventuelle

On peut utiliser ces mêmes fichiers pour chercher le cylindre inscrit ayant la plus grande aire. Pour cela, dans Cyl_Cone, on redéfinit V comme aire du convexe C_yl. On diminue la taille de la figure en augmentant les valeurs u pour l'axe (ox) et v pour l'axe (oy). Ces deux variables indiquent le nombre d'unités de l'espace contenues dans les unités graphiques du plan oxy.

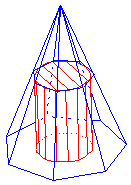
On peut aussi s'intéresser aux cylindres inscrits dans une pyramide comme le suggére la figure ci-contre.

Technique GéoSpace : une seule figure avec deux zones

La technique GéoPlan-GéoSpace d'importation active n'est pas simple à mettre en œuvre.

Dans certains exemples, nous préférons utiliser une seule figure : une zone pour visualiser une situation géométrique, l'autre zone pour tracer une fonction dans un repère (O, i’, j’).

3. Parallélépipède dans une pyramide

Géométrie dans l'espace au bac STI (AA)

Bac national 1999

Avec GéoSpace, charger les deux figures (fermer éventuellement toutes les autres) et les placer en mosaïque (menu : Fenêtres). Mettre la figure graphiq.g3w en mode « Trace », puis pour actualiser les valeurs, rendre active la figure cub_pyr.g3w.

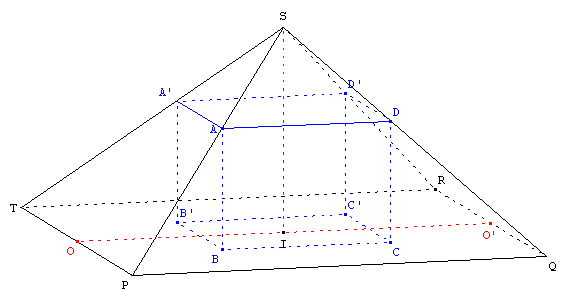
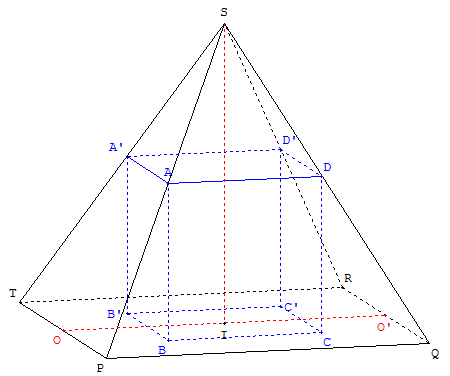
Un fabricant veut commercialiser un produit qui a la forme d'un parallélépipède rectangle à base carrée, dans un emballage qui a la forme d'une pyramide régulière à base carrée (voir la représentation). Les carrés PQRT et BCC’B’ ont même centre I et leurs côtés sont deux à deux parallèles.

Télécharger la figure GéoSpace para_pyr.g3w, télécharger la figure GéoSpace graphiq.g3w

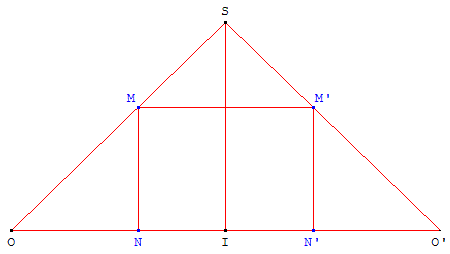
BC = NN’ = 8
BA = NM = 6
OO’ = PQ = x
SI = h

Le but du problème est de trouver les dimensions de la pyramide de telle sorte que son volume soit minimal.

Le fabricant ne veut pas que la longueur PQ du côté de la base de la pyramide soit supérieure à 20 cm.

Les dimensions du parallélépipède sont 8 cm pour le côté [BC] de la base carrée et de 6 cm pour la hauteur [BA].

On désigne par x la longueur du côté [PQ] de la base de la pyramide et par h la longueur de sa hauteur [IS], où S est le sommet de la pyramide.

Télécharger la figure GéoSpace cub_py1.g3w

Partie A

On rappelle que le volume d'une pyramide est V = (B×h) où B est l'aire de sa base et h sa hauteur.

1. Entre quelles valeurs extrémes le nombre x peut-il varier ?

2. Exprimer h en fonction de x . (on pourra se placer dans le plan (OSO’).)

3. En déduire une expression du volume V(x) de la pyramide.

Partie B

Soit f la fonction définie sur l'intervalle ]8, 20] par f(x) = .

1. Démontrer que sur l'intervalle ]8, 20], la dérivée de f est définie par :

f’(x) = .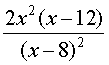

2. étudier les variations de la fonction f.

3. Construire la courbe représentative de f dans un plan muni dans un repère (O, , ) (unités graphiques : 1 cm pour 1 cm en abscisse, 2 cm pour 100 cm³ en ordonnée).

Partie C

1. Montrer que pour tout x ∈ ]8, 20] : V(x) = 2 f(x).

2. En déduire la valeur de x pour laquelle le volume de la pyramide est minimal ?

3. Quel est alors ce volume ? Quelle est la hauteur de la pyramide ? Quel est le volume à remplir entre le produit et l'emballage ?

Éléments de correction

Partie A

1. Le côté de la base de la pyramide est supérieur au côté de celle du parallélépipède donc x>8 et x ∈ ]8, 20].

2. Dans le triangle OSI, rectangle en I, du plan (OSO’) on a : tan SÔI = .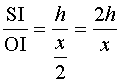

De même, dans le triangle OMN, rectangle en N : tan MÔN = = = .

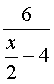De l'égalité (de Thalès) = on déduit = , soit h = .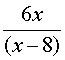

3. Le volume de la pyramide V(x) = B × h = x² × 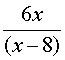= = 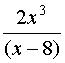2 f(x).

Partie B

Soit f la fonction définie sur l'intervalle ]8, 20] par f(x) = .

1. Sur l'intervalle ]8, 20], la dérivée de f est : f’(x) = .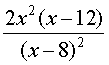

f’(x) est du signe de (x - 12).

2. Tableau de variations de la fonction f :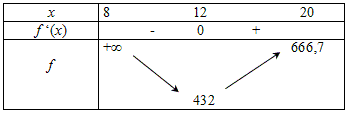 

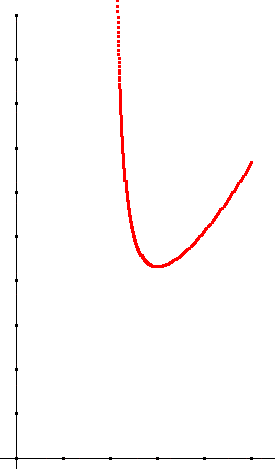
3. Courbe représentative de f : 4 cm pour une unité sur (Ox) ; 100 cm3 par unité sur (Oy).

Partie C

1. On a montré question 3. de la partie A que pour tout x ∈ ]8, 20] : V(x) = 2 f(x).

2. Le volume de la pyramide est minimal pour x = 12.

3. Ce volume est V(12) = 864 cm³. La hauteur de la pyramide est alors h = 18 cm.

Le volume à remplir entre le produit et l'emballage est V(12) - 8²× 6 = 480 cm³.

Variante : cube dans une pyramide

Avec BA = BC = 6, on peut remplacer le parallélépipède rectangle par un cube à inscrire dans une pyramide.

Volume minimal d'une pyramide régulière à base carrée contenant un cube

Figures 3D dans GeoGebraTube Figure de base : cube sur carré

Réalisation : cube dans pyramide

Table des matières

Avec GéoSpace

Dans d'autres pages du site

Sections de cube et pyramide en 3^e

GeoGebra 3D en 2^nde Incidence

GeoGebra 3D : Sections de tétraèdre

GéoSpace Activités

L'espace à l'épreuve pratique 2009

Longueur minimum en 3^e

1S - TS : Problèmes d'optimisation

Téléchargement

 Télécharger geospace_fonction.doc : ce document au format « .doc »

Google considère l'URL originale comme une erreur de type "soft 404".

Google friendly