René Descartes GeoGebra Descartes et les Mathématiques

Tétraèdre avec GeoGebra 3D

La géométrie dans l'espace en seconde tétraèdre orthocentrique

Sommaire

1. Tétraèdres particuliers

2. Tétraèdre ayant des hauteurs concourantes

3. Tétraèdre orthocentrique

4. Cas particulier : tétraèdre régulier

5. Tétraèdre et orthogonalité

6. Tétraèdre tronqué

0. Tétraèdre - Définition

Les tétraèdres sont des polyèdres de la famille des pyramides,
composés de 4 faces triangulaires, 6 arêtes et 4 sommets

Dans l'espace, un 3-simplexe est l'objet le plus simple à 3 dimensions ;
c'est un : tétraèdre.

1. Tétraèdres particuliers

Figure 3D dans GeoGebraTube : tétraèdre libre

Définitions :
les médianes d'un tétraèdre sont les segments reliant
les sommets au centre de gravité de la face opposée.

Les quatre médianes sont concourantes au centre de
gravité du tétraèdre,
situé aux , à partir du sommet, de chaque médiane.

Bimédiane
Dans un tétraèdre, on appelle bimédianes les droites
passant par les milieux de deux arêtes opposées.
Les trois bimédianes sont concourantes au centre de gravité.

Figures 3D dans GeoGebraTube :
bimédianes d'un tétraèdre

Voir équibarycentre de quatre points

1.a. Tétraèdre de base un triangle équilatéral

Geogebra 3d - tétraèdre de base un triangle équilatéral - copyright Patrice Debart 2015

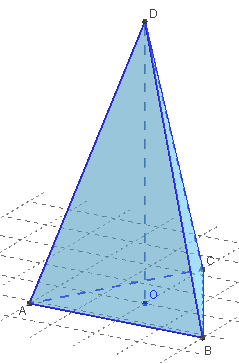
Base du tétraèdre : un triangle équilatéral de côté a
de hauteur : hauteur et de centre O.

Outils GeoGebra :
Construction à partir de deux points A et B du
PlanxOy, tels que AB = a, et de la hauteur.

Construction du point C et du triangle équilatéral ABC:
ABC = Polygone[A, B, 3]
et construction de la pyramide de base ABC et avec la
hauteur : ABCD = Pyramide[ABC, hauteur].

Case à cocher : technique GeoGebra

Créer, et afficher dans la fenêtre graphique, un booléen o=false

Dans le dernier onglet des
propriétés de cette variable,
saisir le script par actualisation :

SoitValeur[hauteur,a*sqrt(2/3)]
SoitValeur[o,false]

Lorsque l'on clique dans la case à cocher, la hauteur
devient a, celle du tétraèdre régulier.
La transformation effectuée, le script remet la case
à cocher à false, ce qui permet de modifier ensuite
hauteur sans ambiguïté.

Figure 3D dans GeoGebraTube :
tétraèdre de base un triangle équilatéral

1.b. Tétraèdre régulier

Geogebra 3d - tétraèdre régulier - copyright Patrice Debart 2015

ABCD est un tétraèdre régulier.
Les six arêtes sont de même longueur a.
Les quatre faces sont des triangles équilatéraux.

Figures 3D dans GeoGebraTube : tétraèdre régulier

Calcul de la hauteur d'un tétraèdre régulier

Les quatre hauteurs sont de longueur h = AH = a
(calcul dans le triangle isocèle BB’D où BB’est la
médiane du triangle équilatéral BCD de côtés a.
BA’ = a et le centre de gravité H est aux deux tiers
de BA’ :

BH = a, puis conclure avec Pythagore, dans le
triangle rectangle ABH).

Les hauteurs sont aussi médianes, concourantes au
centre de gravité O, situé au quart de HA : HI = HA.

Le centre de gravité I est aussi l'orthocentre
du tétraèdre et est équidistant des sommets.
C'est le centre de la sphère dans laquelle est
inscrit le tétraèdre.
Un tétraèdre régulier est orthocentrique.

Volume d'un tétraèdre

V = × aire de la base × hauteur = × A_base × h.

Calcul du volume d'un tétraèdre régulier

V = A_base× h = a² × a = a³.

1.c. Tétraèdre trirectangle

Geogebra 3d - tétraèdre trirectangle - copyright Patrice Debart 2015

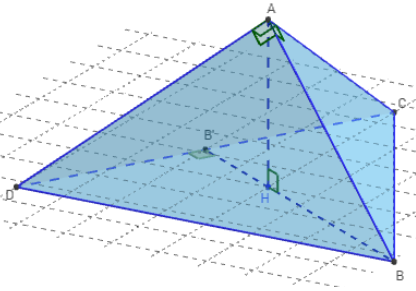
On dit aussi que ABCD est un tétraèdre rectangle isocèle.

La base est un triangle équilatéral,
les trois faces latérales sont des triangles rectangles isocèles.

Le sommet A est l'orthocentre du tétraèdre qui orthocentrique.

Figures 3D dans GeoGebraTube :
tétraèdre trirectangle

Calcul des longueurs des côtés, d'une médiane et de la hauteur

Si a est la longueur des côtés de la base BCD, la
longueur des petits côtés des triangles
rectangles est AB = a.
De la longueur BB’ = a d'une médiane du triangle équilatéral,
on déduit BH = a.
Par la propriété de Pythagore dans le triangle ABH,
rectangle en H, la hauteur du tétraèdre est donc AH = a.

Coin de cube

Le tétraèdre trirectangle ABCD est le coin
d'un cube ABECDB’E’C’ de côté c = a .

L'aire base S_ABC est égale à la moitié de celle du côté
du cube, soit S_ABC = c^2,, et la hauteur AD = c.
Le volume est : V = S_ABC × c = c³.

Le volume du tétraèdre trirectangle est
un sixième du volume du cube qu'il engendre.

Dans la figure tétraèdre régulier inscrit dans un cube on
vérifie ce calcul par la décomposition d'un cube en un
tétraèdre régulier de volume égal au tiers de celui du
cube et de quatre coins de cube.

Figures 3D dans GeoGebraTube : coin de cube

2. Tétraèdre ayant des hauteurs concourantes

Soit ABCD un tétraèdre non plat. On projette
orthogonalement les sommets sur les faces
opposées ; on obtient respectivement les points H, P, Q, R.

Figures 3D dans GeoGebraTube :
quatre hauteurs d'un tétraèdre

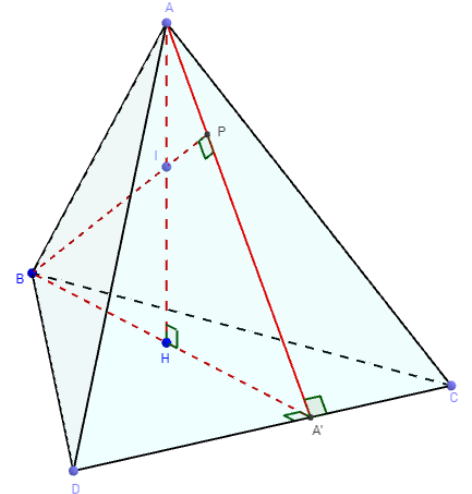
Si deux hauteurs sont concourantes, l'arête qui joint les
sommets est orthogonale à l'arête opposée

Si deux hauteurs (AH) et (BP) sont concourantes
en I, alors les arêtes (AB) et (CD) sont orthogonales.

Geogebra 3d - tétraèdre avec 2 hauteurs concourantes - copyright Patrice Debart 2015

En effet, les droites (AP) et (BH) situées dans le plan
(ABI) se coupent en A’. Comme (AP) est sur la face
(ACD) et (BH) sur la face (BCD), le point A’
appartient à la droite (CD) intersection de ces deux plans

(AH) étant perpendiculaire au plan (BCD), le plan
(ABA’) qui contient (AH) est perpendiculaire au
plan (BCD). De même, la droite (BP) étant
perpendiculaire au plan (ACD), le plan (ABA’)
qui contient (BP) est perpendiculaire au plan (ACD).

Le plan (ABA’), perpendiculaire aux deux plans
(BCD) et (ACD) est perpendiculaire à leur
intersection, la droite (CD).
La droite (AB) contenue dans le plan (ABA’) est orthogonale à (CD).

Remarque : les droites (AA’) et (BA’) contenues dans le
plan (ABA’) sont perpendiculaires à (CD). Ce sont les
hauteurs des faces (ACD) et (BCD).

Réciproquement, si les arêtes (AB) et (CD) sont
orthogonales, alors les hauteurs (AH) et (BP)
sont concourantes

En effet, le plan perpendiculaire à (CD), passant par A,
contient la droite (AB).
Ce plan coupe (CD) en un point A’.
Le plan (ABA’), perpendiculaire à la droite (CD),
est perpendiculaire au plan (BCD) qui la contient.
La hauteur (AH) perpendiculaire à (BCD)
est donc contenue dans le plan (ABA’).

De même, la hauteur (BP) est contenue dans le
plan (ABA’), car cette droite et ce plan sont
tous deux perpendiculaires au plan (ACD).

Les hauteurs (AH) et (BP) contenues dans le même plan (ABA’)
sont concourantes (elles ne sont pas parallèles).

Figures 3D dans GeoGebraTube :
tétraèdre ayant deux hauteurs concourantes
Problèmes : p planxOy définit courbe implicite et
avec intersectionChemin[p,q]. Cliquer sur OK !

Si deux arêtes sont orthogonales, les paires de hauteurs,
issues des deux sommets de chaque arête, sont
concourantes et les deux points de concours
sont situés sur la bimédiane, perpendiculaire
commune à ces arêtes

Geogebra 3d - tétraèdre avec 2 paires de hauteurs concourantes - copyright Patrice Debart 2015

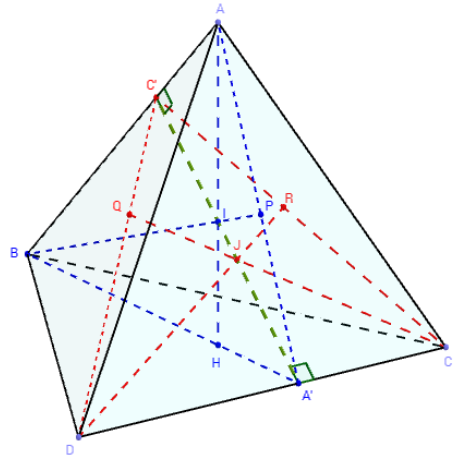
Par dualité, comme les arêtes (AB) et (CD) sont
orthogonales, alors les hauteurs (CQ) et (DR)
sont concourantes en J.

Le plan (CDJ) coupe la droite (AB) au point C’
qui est l'intersection des droites (CR) et (DQ).

Les plans (ABA’) et (CDC’) ont pour intersection
la droite (A’C’) qui contient les points I et J.

La droite (A’C’) est perpendiculaire à (AB) car
contenue dans le plan (CDC’) perpendiculaire
à (AB). (A’C’) est une hauteur du triangle ABA’.
De même, cette droite (A’C’) contenue dans
le plan (ABA’) est perpendiculaire à (CD) et
est une hauteur du triangle CDC’.

La droite (A’C’) est donc la perpendiculaire commune à (AB) et (CD),
A’C’ est la plus courte distance de ces deux arêtes.

Les points I et J sont situés sur la perpendiculaire
commune aux arêtes (AB) et (CD).

Figures 3D dans GeoGebraTube :
deux arêtes orthogonales d'un tétraèdre

Le calcul du carré de l'hypoténuse dans les triangles
rectangles CAA’ et DAA’ permet d'écrire :
AA’² = CA² + CA’² = DA² + CA’².

De même, dans les triangles rectangles CBA’ et DBA’,
on a : BA’² = CB² + CA’² = DB² + DA’².
Par différence DA’² - CA’² = CA² - DA² = CB² - DB².

Relation métrique : CA² + DB² = CB² + DA².

Autre méthode : produit scalaire en terminale

Technique GeoGebra 3D : A, B et C sont trois points
libres de l'espace, D est un point libre dans le plan
perpendiculaire à (AB) passant par C.

3. Tétraèdre orthocentrique

Quatre hauteurs concourantes d'un tétraèdre

Geogebra 3d - tétraèdre orthocentrique - copyright Patrice Debart 2015

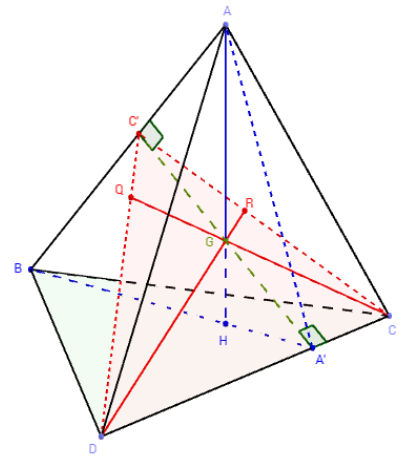
Définition : un tétraèdre orthocentrique a ses quatre
hauteurs concourantes.
Le point de concours est alors l'orthocentre du tétraèdre.

Propriétés :

• Un tétraèdre orthocentrique a ses arêtes opposées
orthogonales deux à deux.
• Les quatre hauteurs sont concourantes en G
orthocentre du tétraèdre.
Le point G est aussi le point de concours des trois
bimédianes, perpendiculaires communes aux
couples d'arêtes opposées.
• Les pieds des hauteurs sont les orthocentres des
faces opposées.
• La somme des carrés des longueurs de deux arêtes
opposées est la même pour chacune des trois
paires d'arêtes opposées :
Pour un tétraèdre ABCD on a :
AB² + CD² = CA² + DB² = CB² + DA².

Le but de cette activité est de montrer qu'une des
quatre propriétés suivantes est suffisante pour
caractériser un tétraèdre orthocentrique :

• Deux couples d'arêtes opposées sont orthogonales,
• Trois des hauteurs sont concourantes,
• Le pied d'une des hauteurs est l'orthocentre de la face opposée,
• AB² + CD² = CA² + DB² = CB² + DA².

Technique GeoGebra 3D : Pour tracer un tétraèdre
orthocentrique, placer trois points A, B et C libres de
l'espace, et un point D libre sur la droite (d)
intersection des plans orthogonaux à (AB) passant par C
et à (BC) passant par A (la droite (d) est la
perpendiculaire au plan (ABC) passant par
l'orthocentre du triangle ABC).

Figure 3D dans GeoGebraTube : tétraèdre orthocentrique

3.b. Deux couples d'arêtes opposées orthogonales

Propriété caractéristique : un tétraèdre qui a deux couples
d'arêtes opposées orthogonales est orthocentrique

Soit ABCD un tétraèdre dont les arêtes opposées [AB]
et [CD] soient orthogonales ainsi que [BC] et [AD].

3.b.a. La hauteur (AH) est perpendiculaire au (BCD)
donc orthogonale à la droite (CD) contenue dans ce
plan. La droite (CD) est orthogonaleà (AB) par
hypothèse. Le plan (ABH), qui contient ces droites
(AB) et (AH), est perpendiculaire à (BC).
La droite (BH) contenue dans ce plan est
perpendiculaire à (CD) : c'est une hauteur du triangle BCD.

3.b.b. De même, la droite (BC) est orthogonale à la
hauteur (AH) et à (AD) par hypothèse, donc
perpendiculaire au plan (ADH). La droite (DH)
contenue dans ce plan est perpendiculaire à (BC) :
c'est une deuxième hauteur du triangle BCD.

Le point H, situé sur deux hauteurs,
est l'orthocentre du triangle BCD.
Le pied H de la hauteur (AH) du tétraèdre
est l'orthocentre de la face (BCD).

3.b.c. Les quatre hauteurs du tétraèdre sont
concourantes en G orthocentre du tétraèdre.

Les arêtes opposées [AB] et [CD] sont orthogonales,
d'après le paragraphe a.
Les hauteurs (AH) et (BP) sont concourantes en I,
et les hauteurs (CQ) et (DR) sont concourantes en J,
I et J étant sur la perpendiculaire commune (A’C’).

Les arêtes opposées [BC] et [AD] sont orthogonales, les hauteurs
(AH) et (DR) sont concourantes en K, le plan (ADH) contient
les droites (AH) et (DR), les points I et J.

La droite (A’C’) n'est pas incluse dans le plan (ADH), l'intersection
avec plan est réduite à un point G. Les points I et J,
communs à (ADH) et à (A’C’) sont confondus en G.

3.c. Première réciproque :

Un tétraèdre à 3 hauteurs concourantes est orthocentrique

Les hauteurs (AH), (BP) et (CQ) d'un tétraèdre ABCD sont concourantes.
Montrer que le tétraèdre est orthocentrique

Solution

Les deux hauteurs (AH) et (BP) sont concourantes
en G, les arêtes (AB) et (CD) sont orthogonales.
Les deux hauteurs (AH) et (CQ) sont concourantes
en G, les arêtes (AC) et (BD) sont orthogonales.
Deux couples d'arêtes opposées sont orthogonales.
Le tétraèdre ABCD est orthocentrique.

3.d. Deuxième réciproque :

Le pied d'une hauteur est l'orthocentre de la face opposée

Geogebra 3d - tétraèdre - pied d'une des hauteurs - copyright Patrice Debart 2015

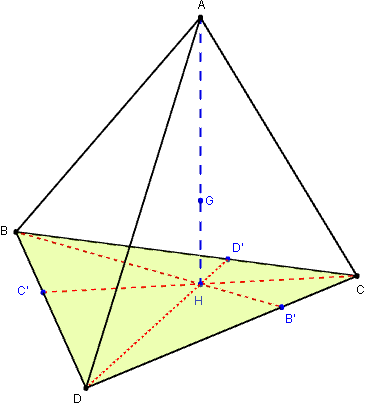
Soit ABCD un tétraèdre, tel que la projection
orthogonale H du sommet A sur la face (BCD)
soit l'orthocentre du triangle BCD.

Montrer que la droite (BC) est orthogonale à (AH) et
perpendiculaire à (HD),
en déduire que (BC) est orthogonale à (AD),
conclure que le tétraèdre est orthocentrique.

Figures 3D dans GeoGebraTube :
pied de hauteur orthocentre de la base du tétraèdre

Solution

Geogebra 3d - pied d'une des hauteurs d'un tétraèdre - copyright Patrice Debart 2015

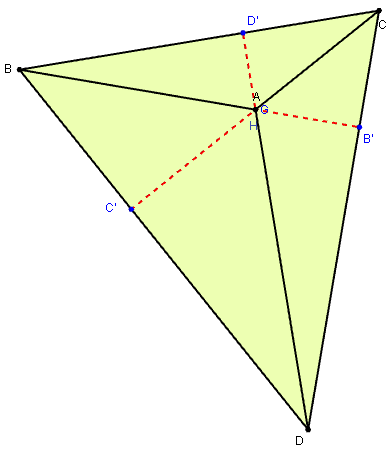
La droite (AH), orthogonale au plan (BCD),
est orthogonale à toutes les droites de ce plan donc à la droite (BC).
H étant l'orthocentre du triangle BCD, (DH) hauteur
issue de D est perpendiculaire au côté (BC).

Le plan (ADH) contient les droites (AH) et (DH).
Ces deux droites distinctes et sécantes en H ne sont pas parallèles
elles sont orthogonales à la droite (BC),
donc la droite (BC) est orthogonale au plan (ADH).
Cette droite (BC), orthogonale au plan (ADH),
est orthogonale à toutes les droites de ce plan, donc à la droite (AD).

Les droites (BC) et (AD) sont orthogonales.

Une démonstration identique montrerait que (CD) et (AB) sont orthogonales.
Le tétraèdre ABCD est orthocentrique ;
les arêtes (BD) et (AC) sont aussi orthogonales.

Avec GeoGebra 3D, créer une vue avec le plan BCD
de face pour visualiser ces orthogonalités.

3.e. Groupe orthocentrique

Les quatre sommets A, B, C, D, d'un tétraèdre
orthocentrique, et l'orthocentre H forment un
groupe orthocentrique de cinq points A, B, C,
D, H, tels que la droite qui joint deux
quelconques d'entre eux est orthogonale au plan formé par les trois autres.

Voir aussi : groupe orthocentrique dans le plan

3.f. Droites entre les côtés opposés du tétraèdre

Geogebra 3d - perpendiculaires communes dans un tétraèdre orthocentrique - copyright Patrice Debart 2015

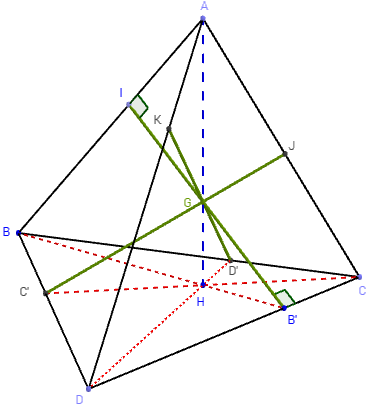
Trois perpendiculaires communes

Les bimédianes (IB') ; (JC') et ( KD') sont
concourantes au point G, orthocentre du tétraèdre.

Dans ce tétraèdre orthocentrique on appelle B', C', D', I,
J et K, les pieds respectifs des hauteurs des faces.

Les droites IB'; JC 'et KD' sont les perpendiculaires
ommunes aux arêtes opposées.

Elles représentent la distance entre deux arêtes.

Ambiguïté : Dans cette figure G représente
l'orthocentre, dans celle droite, G est le centre gravité !

Par contre, dans le tétraèdre régulier, ces deux points
sont confondus au centre du tétraèdre.

Figures 3D dans GeoGebraTube :
perpendiculaires communes du tétraèdre orthocentrique

Bimédianes du tétraèdre orthocentrique

Geogebra 3d - bimedianes dans un tétraèdre orthocentrique - copyright Patrice Debart 2015

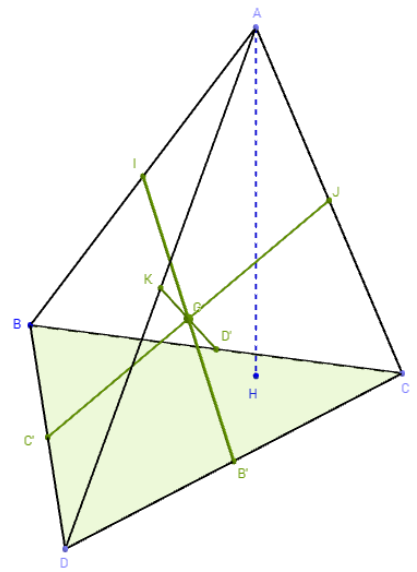
Relations métriques

On considère un tétraèdre orthocentrique ABCD.

On appelle B', C', D', I, J et K les milieux des
arêtes [AB], [CD], [BC], [AD], [AC] et [BD].

3.f.a. Déterminer la nature du quadrilatère IJB'C'.
3.f.b. Démontrer que les trois bimédianes, segments
ayant pour extrémités les milieux des arêtes opposées, ont même longueur a.
3.f.c. Démontrer que la somme des carrés des
longueurs de deux arêtes opposées est égale à 4a².

Indications

3.f.a. IJB'C' est un rectangle.

3.f.b. Les diagonales d'un rectangle sont égales :
IB' = JC' = KD' = a ;
a est aussi la distance entre deux arêtes opposées.

3.f.c. Calculer par différence, comme au paragraphe 2 :
« tétraèdre ayant des hauteurs concourantes » ; on trouve :
AB² + CD² = CA² + DB² = CB² + DA² = 4a².

Figures 3D dans GeoGebraTube :
bimédianes d'un tétraèdre orthocentrique

Voir réciproque en terminale S : produit scalaire dans l'espace

Relation vectorielle

ABCD est un tétraèdre. On appelle I et B'
les milieux respectifs des arêtes [AB] et [CD].

Démontrer que + = + = 2vect(I,B').

4. Cas particulier : tétraèdre régulier

Perpendiculaire commune dans un tétraèdre régulier

Geogebra 3d - perpendiculaire commune dans un tétraèdre oerthocentrique - copyright Patrice Debart 2015

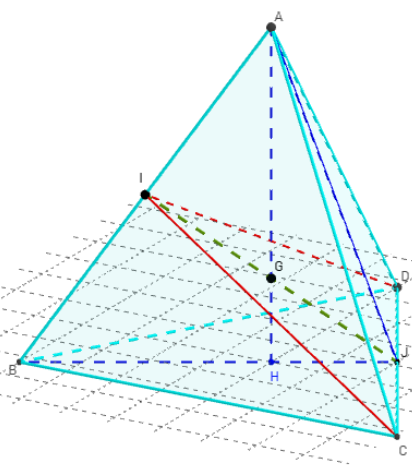
ABCD est un tétraèdre, dont toutes les faces
sont des triangles équilatéraux.
On appelle I et J les milieux respectifs des arêtes [AB] et [CD].
Démontrer que les arêtes opposées (celles
qui ne se coupent pas) sont orthogonales.
Montrer que la bimédiane (IJ) est la
perpendiculaire commune aux droites (AB) et (CD).

Solution

Le fait que toutes les faces soient des triangles
équilatéraux devant être utilisé, considérons le
milieu J de [CD]. BCD est un triangle équilatéral,
la médiane (BJ) est aussi hauteur, donc (BJ) est perpendiculaire à (CD).
De même, puisque le triangle ACD est équilatéral,
la médiane (AJ) est perpendiculaire à (CD).
Le plan (ABJ) contient donc deux droites sécantes
perpendiculairesà (CD) ; la droite (CD) est par
conséquent orthogonale au plan (ABJ).
La droite (CD) est alors orthogonale à toutes les droites
du plan (ABJ).
Elle est en particulier orthogonale à la droite (AB), contenue dans ce plan.

Les droites (AB) et (CD) sont orthogonales.
Une démonstration identique montrerait que (AD) et
(BC), ainsi que (AC) et (BD) sont orthogonales.

Figures 3D dans GeoGebraTube :
centre du tétraèdre régulier

Voir : sections planes du tétraèdre

Par ailleurs, la droite (CD), orthogonale à toutes les
droites du plan (ABJ), est orthogonale à la droite
(IJ) contenue dans ce plan : (CD) est perpendiculaire à (IJ).
Une étude analogue montrerait que la droite (AB)
est orthogonale au plan (CDI) et quelle est donc
orthogonale à la droite (IJ), contenue dans ce plan :
(AB) est perpendiculaire à (IJ).
La droite (IJ) est la perpendiculaire commune aux droites (AB) et (CD).

5. Tétraèdre et orthogonalité

Tétraèdre inscrit dans une sphère

Geogebra 3d - tétraèdre inscrit dans une sphere - copyright Patrice Debart 2015

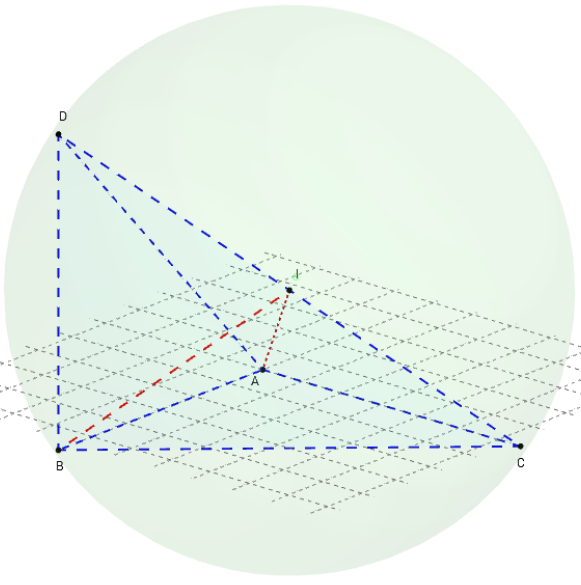
Dans un plan (p) on considère le triangle ABC rectangle en A.
Soit (d) la droite passant par B et orthogonale à (p).
On considère un point D de (d) distinct de B.

1. Montrer que les faces du tétraèdre ABCD sont des triangles rectangles.

2. Montrer que les sommets du tétraèdre sont équidistants du milieu I de [CD].

Indications

[AI] est la médiane issue du l'angle droit du triang
le rectangle ADC, donc AI = CD/2, de même,
pour la médiane [BI] du triangle rectangle BDC,
on a BI = CD/2.

Le tétraèdre est inscrit dans la sphère de diamètre [CD].

Figures 3D dans GeoGebraTube :
tétraèdre inscrit dans une sphère

6. Tétraèdre tronqué

Geogebra 3d - tétraèdre tronqué - copyright Patrice Debart 2015

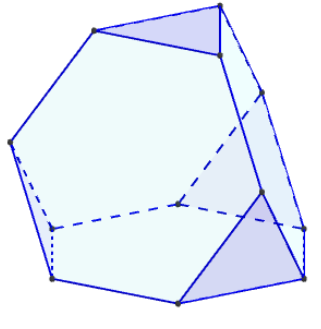
Sur chaque arête d'un tétraèdre régulier,
placer les deux points situés au tiers et aux deux tiers du côté.

Le solide ayant pour sommets ces douze points est un tétraèdre tronqué.

C'est un polyèdre semi-régulier dont quatre des huit
faces sont des triangles équilatéraux, les autres
faces étant quatre hexagones réguliers.

Le tétraèdre tronqué est un des 13 solides d'Archimède.

Technique GeoGebra

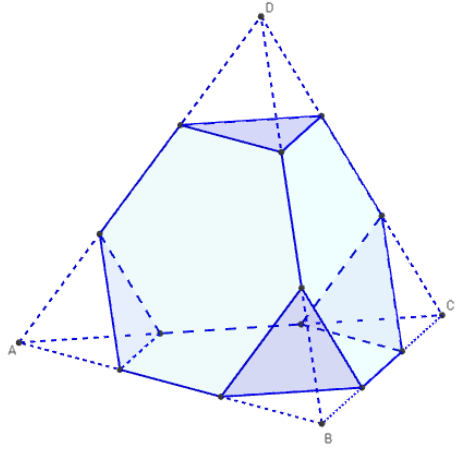
Dans GeoGebra il n'existe pas de repère sur une droite.
Pour placer les points A₁ et B₁ aux et de [AB],
utiliser des barycentres et écrire dans la ligne de saisie :
A₁ = (2A + B)/3 et B₁ = (A + 2B)/3