Descartes et les Mathématiques

Problèmes d'optimisation avec la géométrie dynamique

Exercices à prise d'initiative - de nombreuses situations menant à des problèmes d'optimisation.

Sommaire

1. Arc de cercle ?

2. Tangente à la parabole et aire minimum

3. Triangle rectangle isocèle avec contraintes

4. Lieux géométriques avec une rotation et une similitude

Problèmes d'optimisation en classe de première

1. Arc de cercle ?

ÉduSCOL - Terminale S - Banque de sujets 2004 - Sujet 4 

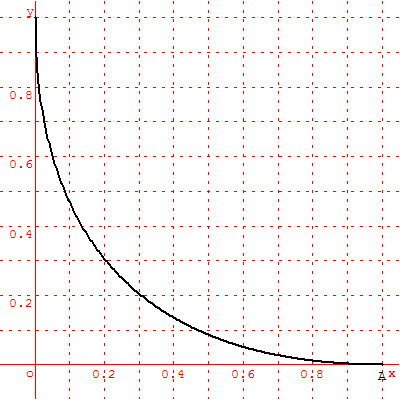
Soit f  la fonction définie sur l'intervalle [0 ; 1] par :
f(x) = x - 2 + 1.

La courbe représentative Γ de la fonction f dans un repère orthonormal est donnée ci-contre.

  • Montrer que le point M de coordonnées (x, y) appartient à Γ si et seulement si x ≥ 0, y ≥ 0 et + = 1.

  • Montrer que Γ est symétrique par rapport à la droite d'équation y = x.

  • Si Γ était un arc de cercle, quel pourrait être son centre?
Quel pourrait être son rayon ?

  • La courbe Γ est-elle un arc de cercle ?

De l'équation y = x - 2 + 1, on trouve y = (1 - )².
Comme 0 ≤ x ≤ 1, alors 0 ≤ ≤ 1 et 0 ≤ y ≤ 1 et on peut calculer la racine carrée :
= 1 - soit + = 1.

Cette équation est symétrique en x et y : si un point M(x, y) appartient à Γ, alors
M’(y, x) est aussi sur Γ.
L'axe (O, + ) d'équation y = x est axe de symétrie de la courbe.

Cette droite coupe Γ au point C tel que 2 = 1 donc x = y = .

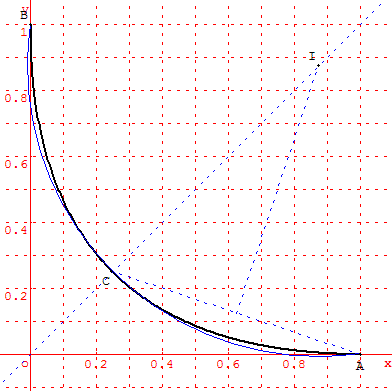
Si Γ était un arc de cercle, il passerait par A, B et C.
Son centre I serait situé sur l'axe (O, + ), médiatrice de [AB], et sur la médiatrice de [AC].
Cette dernière droite, perpendiculaire à (- , - ) en J(, ), a pour coefficient directeur 3 et pour équation :
y = 3x - . Les deux médiatrices se coupent au point K tel que x = y = .

Commandes GéoPlan

Taper S pour visualiser un arc de cercle de centre I, situé sur la première bissectrice des axes, et passant par les points A(1, 0) et B(0, 1).
Taper C pour placer le point I au point K de coordonnées (, ), centre du cercle passant par A, B et C.

Quel que soit le centre I, la courbe Γ et l'arc de cercle sont distincts.

GéoPlan permet de visualiser la parabole contenant Γ.

Justification

De l'équation y = x - 2 + 1, on trouve 2 = x - y + 1 et en élevant au carré :
4x = (x - y + 1)² = x² + y² - 2xy + 2x - 2y + 1.

Le terme 2xy de l'équation x² + y² - 2xy - 2x - 2y + 1 = 0 fait que Γ n'est pas un arc de cercle, mais un arc de conique, plus particulièrement de parabole.

Démonstration

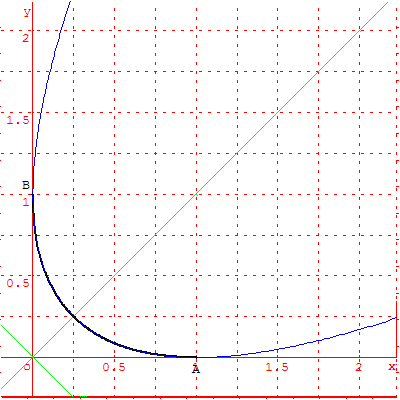
En raison de la symétrie, on est donc amené à étudier la courbe dans le nouveau repère (O, , ) avec : = - et = +

Pour un point M(x, y) dans le repère (O, , ) on a : = x + y , dans le nouveau repère M a pour coordonnées (X, Y) avec = X + Y .

X + Y = X ( - ) + Y( + ) = X - X + Y + Y = (X + Y) + (Y - X).
En identifiant avec x + y , on trouve les formules de changement de variable :
x = X + Y
y = Y - X.

Remplaçons par les nouvelles coordonnées dans l'équation :
(X + Y)² + (Y - X)² - 2 (X + Y)(Y - X) - 2(X + Y) - 2(Y - X) + 1 = 0.
Soit 4X² - 4Y + 1 = 0. Γ est un arc de la parabole d'équation Y = X² + .

Télécharger la figure GéoPlan courbe_arc_cercle.g2w

2. Tangente à la parabole et aire minimum

Le plan est muni d'un repère orthonormal (O; , ) d'unité graphique 2cm.

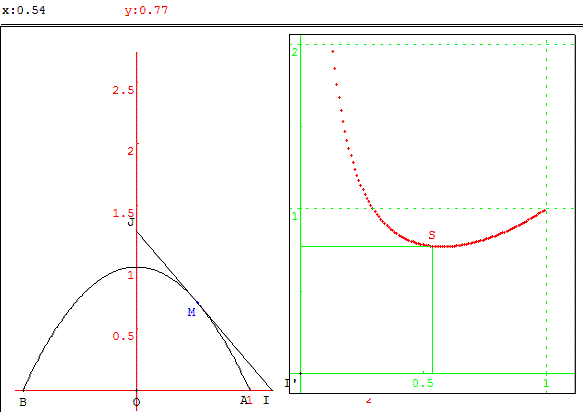
2.a. Soit g la fonction définie sur ]-1, 1[ par g(x) = 1 - x². Tracer la courbe (C) représentative de g.

2.b. Soit x un nombre réel non nul élément de l'intervalle ]0 ; 1]. On appelle M le point de (C) d'abscisse x.
On appelle (T) la tangente en M à la courbe (C).
(T) coupe l'axe des abscisses en I et l'axe des ordonnées en J.

Pour quelle valeur de x l'aire du triangle OIJ est-elle minimum ?

Technique GéoPlan : dans cet exercice est utilisée une seule figure avec deux cadres.

Déplacer le point variable M de la fenêtre de gauche.

Problèmes d'optimisation en terminale

3. Triangle rectangle isocèle avec contraintes

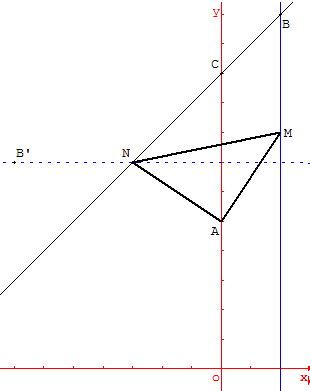
Soit (O ; , ) un repère orthonormal direct du plan.

On considère trois points A, B, C de coordonnées respectives (0, 5) ; (2, 12) ; (0, 10).

On appelle (d₁) la parallèle à l'axe (Oy) passant par B et (d₂) la droite (BC).

Trouver un point M sur (d₁) et un point N sur (d₂) tels que le triangle AMN soit rectangle isocèle direct en A.

Solution

Si le triangle rectangle isocèle AMN existe, le point M est obtenu à partir du point N par une rotation de 90° autour de A. Cela nous donne une méthode de construction du triangle qui répond à la question :
on fait pivoter la droite (d₁) de 90° autour de A. La transformée (d’) coupe (d₂) en N. Le point de (d₁) dont N est l'image est le point M.

4. Lieux géométriques avec une rotation et une similitude

Terminale S

Dans le plan rapporté au repère orthonormal direct (A, , ), on considère le carré ABCD de centre O, soit P un point de [BC].
On appelle N l'image de P par la rotation de centre A et d'angle et M le milieu de [NP].
Déterminer les lieux des points N et M lorsque P décrit [BC].

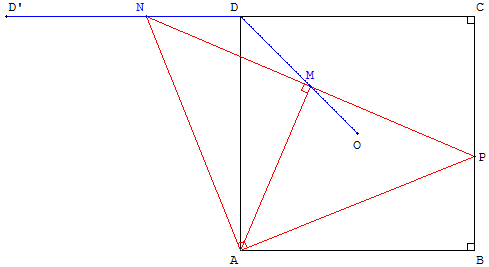
Indications

Soit D’ étant le symétrique de C par rapport à D, D et D’ sont les images de B et C par la rotation.
Le lieu du point N est le segment [DD’] porté par la droite (CD).

Le triangle ANP est rectangle isocèle. M est donc l'image de P par la similitude de centre A, d'angle et de rapport . Les points O et D sont les images de B et C par la similitude.
Le lieu du point M est le segment [OD].

Table des matières

Menu optimisation

Optimisation en troisième

Longueur minimum en 3^e

Optimisation en seconde : Partage d'un trapèze

Dans d'autres pages du site

Optimisation d'une longueur à l'épreuve pratique de TS : voir évacuation des eaux

Études d'aires : minimum-maximum

Huit carrés - Somme de trois angles : voir carrés au collège

Téléchargement

Télécharger optimisation.pdf : ce document au format « .pdf »

Google friendly