Descartes et les Mathématiques

Le carré au collège

Exercices de géométrie dynamique sur le carré :
deux, trois, cinq ou huit carrés.

Sommaire

1. Dessiner un carré

2. Duplication du carré

3. Le carré dans une planche à clous

4. Somme ou différence de deux carrés

    Sulbasutras
      Construction de Bhaskara

      Clairaut

      Puzzle de Gougu

5. Multiplication par 3 de l'aire d'un carré

    Construction d'Abu l-Wafa

6. Triangle rectangle de petits côtés 1 et 2

7. Les trois carrés

8. Huit carrés - Somme de trois angles

1. Construire un carré

Classe de cinquième

1.a. Construction du carré à partir d'un côté

Construction d'Euclide - Proposition 46

Tracer un carré en connaissant deux sommets consécutifs A et B

Tracé du carré à partir de perpendiculaires

Placer deux points A et B et dessiner le segment [AB],
tracer la perpendiculaire à (AB) passant par A et reporter
sur cette perpendiculaire la longueur du côté avec le
cercle de centre A passant par B.
Le sommet D est un des points d'intersection
de cette perpendiculaire et du cercle.

Construire les parallèles à (AB) passant par D et à (AD) passant par B.
Construire le point C comme intersection de ces deux parallèles.

ABCD est un carré de côté [AB].

Variante : après la construction de D, construire
les perpendiculaires à (AB) en B et à (AD) en D.
Construire le point C comme intersection
de ces deux perpendiculaires.

Construction de Marolois : après la construction de D,
construire la perpendiculaire à (AB) en B.
Reporter en C, sur cette deuxième perpendiculaire, la
longueur du côté avec le cercle de centre B passant par A.
Tracer le côté [CD] parallèle à (AB).

1.b. À partir d'un côté et du cercle circonscrit

« Comment tracer un carré au compas ;
Tracer un carré dans un cercle ! »

Construction du carré inscrit dans un cercle

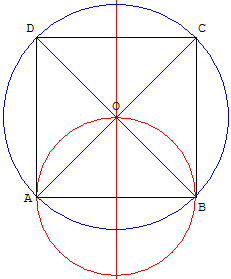
Placer deux points A et B et dessiner le segment [AB],
tracer la médiatrice de [AB] et le cercle de diamètre [AB].

Remarque : avec la règle et le compas, tracer le cercle de
centre A, passant par B, et le cercle de centre B passant par A.
La droite joignant les points d'intersection des deux
cercles est la médiatrice de [AB].

Le centre O du carré est un des points d'intersection
de la médiatrice et du cercle de diamètre [AB].

Le cercle (c) de centre O, passant par A, est le cercle circonscrit au carré.

Le sommet C est le deuxième point d'intersection
de la droite (AO) et du cercle circonscrit (c).
De même, D est l'intersection de (BO) et du cercle (c).

ABCD est un carré de côté [AB] inscrit dans le cercle (c).

Voir : calcul de la longueur du côté d'un carré inscrit dans un cercle

Voir aussi : carré inscrit dans un demi-cercle

1.c. Diagonale du carré

Comment calculer la longueur d'une diagonale d'un carré

Les deux diagonales du carré sont de même longueur,
perpendiculaires et se coupent en leur milieu :
Pour la diagonale [AC], étudier un des triangles
rectangles ABC ou ADC, et y calculer AC  avec
le théorème de Pythagore :

AC² = AB² + BC² = a² + a² = 2 a², pour un carré de côté AB = a.

La longueur d'une diagonale, du carré de côté a, est a.

Construction du carré à partir d'une diagonale

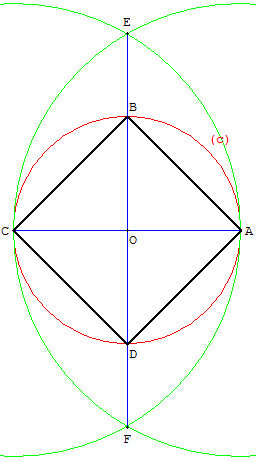
Inscrire un carré dans un cercle de diamètre [AC]
Tracer un carré sans équerre

Placer deux sommets opposés A et C
(ou bien le centre O et un sommet A),
tracer le cercle (c) de centre O, milieu de [AC].
Tracer [AC], diamètre du cercle circonscrit au carré.

Tracer la médiatrice de [AC]. Elle coupe le cercle (c) en B et D.
ABCD est un carré.

Remarque : la règle et le compas permettent de
construire une médiatrice, en traçant le cercle
de centre A passant par C et le cercle de centre
C passant par A, qui se coupent en E et F.
(EF) est la médiatrice de [AC].

Longueur du côté d'un carré inscrit dans un cercle :
en classe de quatrième, on calculera la longueur du côté
du carré avec la relation de Pythagore dans le triangle OAB :
OA² + OB² = AB² ; soit 2r² = AB² ;
d'où AB = r où r est le rayon du cercle (c).

Remarque : La meilleure façon de construire un carré
n'est pas de le générer à partir d'un côté, mais de le
générerà partir d'un centre de rotation O et d'un sommet A.
Le carré ainsi fabriqué est invariant par quart de tour,
a ses côtés égaux et ses angles égaux à 90°.

La figure ci-dessus permet aussi de construire un carré
à partir du cercle circonscrit.

1.d. Sulbasutra

Construction du carré à partir d'une médiatrice

Construction de Baudhayana,
texte rituel de l'Inde védique,
rédigés en sanskrit vers le VIII^e siècle avant J.-C.

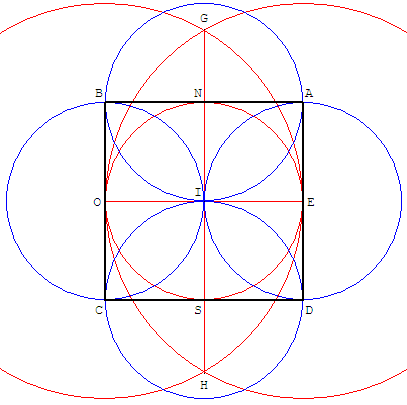
Si l'on veut un carré, prendre une corde de longueur
égale au carré donné, faire des nœuds aux deux
extrémités et une marque en son milieu.
On trace la ligne et on plante un piquet en son milieu.
On fixe les deux nœuds et on trace un cercle avec la marque.

Deux piquets sont plantés aux deux extrémités du diamètre.
Un nœud étant fixé à l'est, on trace un cercle avec l'autre
Même chose à l'ouest.
Le second diamètre est obtenu des points d'intersection
de ces deux ; on plante deux piquets aux deux extrémités du diamètre.

Avec deux nœuds fixés à l'est, on trace un cercle avec la marque ;
on fait la même chose au sud, à l'ouest et au nord.
Les points d'intersection donnent le carré.

Texte en langage moderne

Tracer le diamètre [OE] de longueur le côté du carré a,
et une marque en son milieu I.

Tracer le cercle de centre E et de rayon a. Même chose à
l'ouest avec un cercle de centre O. On obtient les points
d'intersection G et H, et le cercle de centre I et de rayon
a/2 permet d'obtenir le second diamètre [SN].

On trace les cercles de centres E, S, O, N de rayons a/2.
Les points d'intersection donnent le carré ABCD.

1.e. Voir :
construction du carré à la règle (non graduée) et l'équerre

1.f. Aire du carré

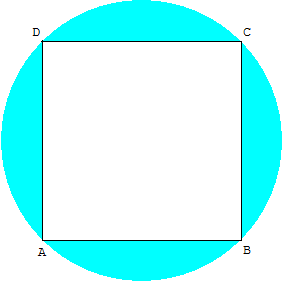
Carré inscrit dans un cercle

ABCD est un carré de côté a = AB et diagonale d = AC.

L'aire du carré de côté a est a².

Calculer la longueur du coté d un carré avec son aire :
a = racine(Aire).

Calcul de l'aire avec la diagonale du carré

d = a, d'où a = d × et Aire(ABCD) = a² = d² × .

L'aire du carré de diagonale d est d².

Calcul d'aire avec un carré inscrit dans un cercle

Le carré ABCD est inscrit dans un cercle de diamètre d.

Vérifier que l'aire de la portion du disque extérieure
au carré (coloriée en bleu clair) est :

d²( – ).

2. Deux duplications du carré

Classe de quatrième

2.a. Tracer à la « règle et au compas » un carré
d'aire double d'un carré donné.

Duplication du carré avec une diagonale

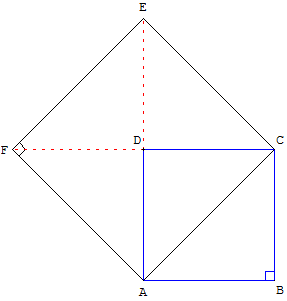
Dans Ménon, un dialogue de Platon, Socrate
explique la construction ci-dessus à un jeune esclave.

La diagonale du « petit carré » le partage en deux
triangles isocèles rectangles. Le « grand carré »
est formé de quatre triangles isocèles
rectangles, de même aire.

Le rapport des aires des carrés est 2,
Le rapport des côtés est .

En terminale S, étudier la similitude de centre A,
d'angle 45° et de rapport .
Elle transforme le carré ABCD en ACEF.

Les carrés de Léonard de Vinci

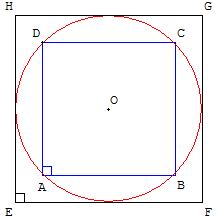
Problèmes de construction

  – À partir d'un point A, construire le carré ABCD
inscrit dans le cercle (c) ;
  – Comme ci-dessous, construire le carré EFGH
circonscrit au cercle (c), les côtés des carrés
parallèles deux à deux.
Comme ci-dessus à gauche, les côtés de EFGH tangents
au cercle en A, B, C et D.

Le carré circonscrit à un cercle a une aire double de celle
du carré inscrit dans ce cercle.

Solution de la duplication de Léonard de Vinci

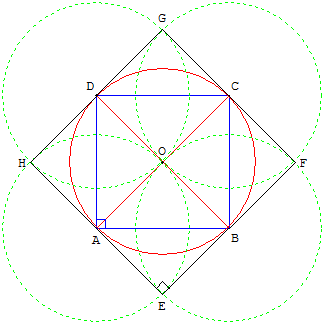
À partir d'un « petit carré » ABCD, de centre O, on trace
les cercles centrés sur les sommets, passant par O.
Ces cercles se coupent en E, F, G, H, symétriques de O
par rapport aux côtés du petit carré. EFGH est un
« grand carré » tangent au cercle circonscrit à ABCD.

Les diagonales du « petit carré » le partagent en quatre
triangles isocèles rectangles. On obtient le « grand
carré » avec quatre autres triangles isocèles rectangles
de même aire, symétriques des quatre premiers.

2.b. Cloître - Carré d'aire moitié

Olympiades 2008 - Toulouse

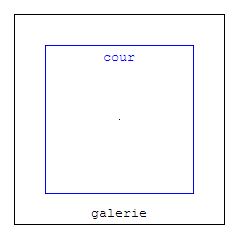
Un cloître est constitué d'une cour intérieure centrale
entourée d'une galerie latérale.

La forme des cloîtres est généralement carrée et,
est telle que l'aire de la galerie est égale à celle de la cour centrale.

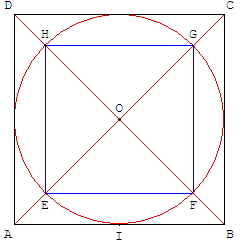
Proposer une méthode permettant de tracer dans l'enclos
un carré délimitant la future cour intérieure centrale du cloître

Tracer les deux diagonales et le centre O du grand carré,
soit I le milieu d'un des côtés du carré, le cercle de
centre O, passant par I, coupe les diagonales aux coins
cherchés de la cour.

En effet, si L est la longueur du côté du grand carré,
le rayon du cercle est .
La diagonale du petit carré mesure L,
la longueur du côté de ce carré est l = ,
son aire l² est bien la moitié de L², aire du grand carré.

3. Le carré dans une planche à clous

Retrouver ces figures GeoGebra dans : la planche à clous

Carré d'aire 2

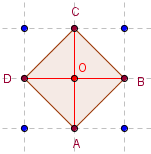
Carré d'aire 2 dans un géoplan 3 × 3

Aire(ABCD) = 4 × = 2.

Les diagonales se coupent en leur milieu O,
sont de même longueur et sont perpendiculaires.

Figure interactive dans GeoGebraTube
        carré dans le géoplan 3 × 3

Carré d'aire 5

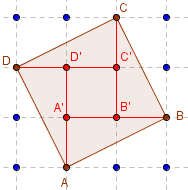
Carré d'aire 5 dans un géoplan 4 × 4

Le carré ABCD, formé du carré central A’B’C’D’
unitaire, et de quatre triangles rectangles
AA’B, BB’C, CC’D, DD’A d'aires 1.

Aire(ABCD) = 1 + 4 × 1 = 5.

Figure interactive dans GeoGebraTube
        Carré dans le géoplan 4 sur 4

Voir, ci-dessous, la figure du moulin à vent

Quatre carrés

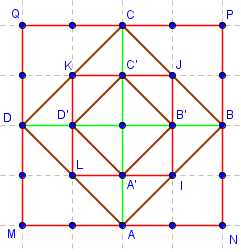
Quatre carrés dans un géoplan 5 × 5

Aire(MNPQ) = 16,
Aire(ABCD) = 8,

Aire(IJKL) = 4,
Aire(A’B’C’D’) = 2.

Figure interactive dans GeoGebraTube
        Carrés du géoplan 5 × 5

Carré d'aire 10

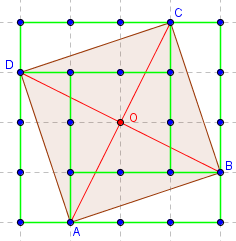
Carré d'aire 10

Aire(ABCD) = 4 + 4 × 1,5 = 10,
Aire(ABCD) = 16 – 4 × 1;5 = 10.

L'aire est obtenue en ajoutant ou en retranchant, à l'aire
d'un carré, les aires de quatre triangles rectangles, d'aires 1,5.

Figure interactive dans GeoGebraTube
        Carré dans le géoplan 5 × 5

4. Carré d'aire la somme des aires de deux carrés

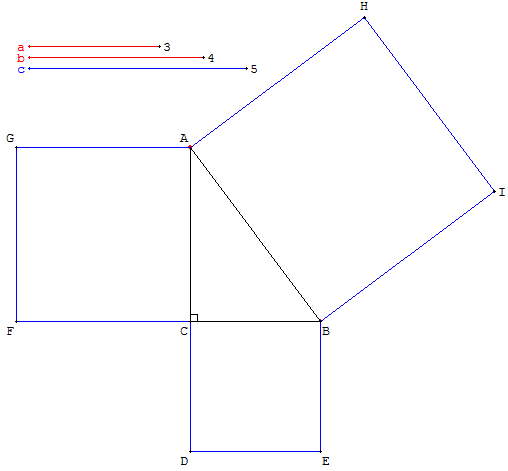
Construire un carré d'aire égale à la somme des aires de deux carrés

4.a. Constructions de carrés d'aire égale à la somme
ou la différence des aires de deux carrés :
applications du théorème de la diagonale.

Variations autour de Pythagore

Théorème de la diagonale (Inde védique)

Le carré produit par la diagonale d'un rectangle est égal
à la somme des carrés produit par les deux côtés du rectangle.

4.b. Carré somme de deux carrés

Dessiner le moulin à vent d'Euclide en traçant deux
carrés CBED et ACFG de côtés a et b à l'extérieur
d'un angle droit en C.
Compléter le triangle rectangle ABC
et construire le carré ABIH de côté AB = c.
Par le théorème de Pythagore, l'aire du grand carré est
égale à la somme des aires de deux carrés.

Indication : déplacer les points A ou B sur les côtés de l'angle droit.

4.c. Différence de deux carrés

Construire un carré d'aire différence de carrés de côtés c et a

Réaliser la figure du moulin à vent avec le tracé d'un carré ABIH de côté c.
Sur le demi-cercle de diamètre [AB], placer le point C
et le long de [AC] construire le carré CBED de côté a.
Compléter le triangle rectangle ABC et construire le carré ACFG de côté b.

L'aire de ce carré est égale à la différence des aires des deux premiers carrés.

4.d. Construction de Bhaskara

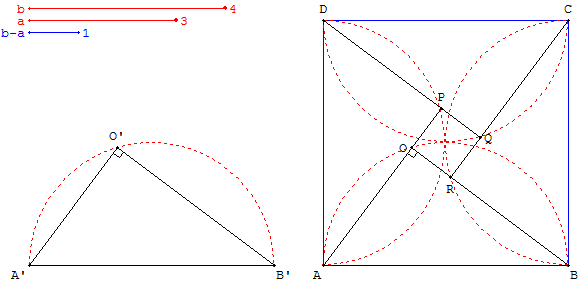
Construire un carré de côté b−a

Construire un triangle rectangle A’O’B’ en O’
tel que O’A’ = a et O’B’ = b, avec b > a.
Construire un carré ABCD, avec un côté de longueur A’B’.
Sur les demi-cercles ayant pour diamètre les côtés du
grand carré, sont placés les points O, P, Q et R formant
les sommets de quatre triangles rectangles du pourtour,
triangles de petits côtés de longueurs a et b.
Le quadrilatère OPQR est un carré de côté de longueur b − a.

4.e. Sulbasutra

Construire un carré somme de deux carrés

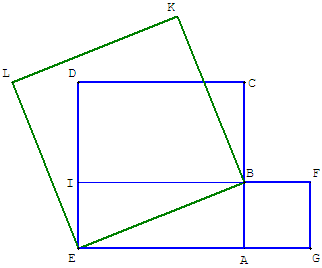
Si l'on rassemble deux carrés de tailles différentes,
que l'on trace à l'aide du côté du plus petit une bande
du plus grand, la corde diagonale de cette bande est
le côté du carré constitué des deux carrés rassemblés.

EB est la longueur du côté du carré d'aire égale à la
somme des aires des carrés contigus ACDE de côté a et ABFG de côté b.

Avec ce que nous appelons le théorème de Pythagore.

Dans le triangle ABE rectangle en A, on a :
EB² = EA² + AB² = a² + b².

4.f. Sulbasutra

Construire un carré différence de deux carrés

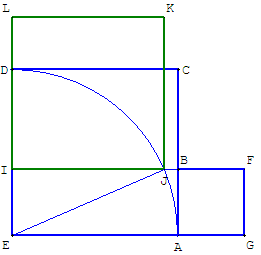
IJ est la longueur du côté du carré d'aire égale à la
différence des aires des carrés contigus ACDE et ABFG.

Justifications

Dans le triangle rectangle IJE, la relation de Pythagore
donne : IJ² = EJ² - IE² = a² - b².

Voir aussi : construction du carré à partir d'une médiatrice

Problème : somme de trois carrés
Construire un carré dont l'aire soit égale à la somme
des aires de trois carrés donnés.

4.g. Carrés contigus

Construction à partir de deux carrés contigus
BCFG et DEHF, de côtés a et b.

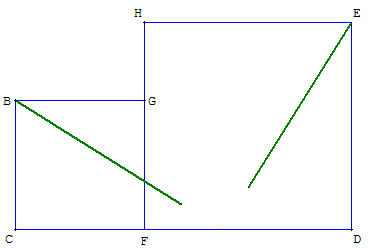
Une recherche guidée par la figure de duplication du
carré ci-dessus permet dans le cas général, aux élèves,
de trouver une solution autour de la diagonale [BE] :

On voit apparaître deux triangles rectangles, on construit
alors un carré et on complète en traçant les verticales
et les horizontales, pour obtenir la figure de Clairaut,
ci-dessous.

Clairaut

Démonstration visuelle du théorème de la diagonale

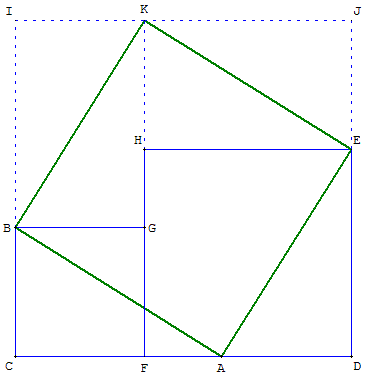
Le carré ABKE de diagonale [BE] est solution.

Justifier cette construction par l'isométrie des triangles
rectangles de sommets C et H, D et G : le triangle CBA
est déplacé en HKE et le triangle DEA est déplacé en GKB

Puzzle de Clairault

Retrouver cette configuration dans : similitude au bac

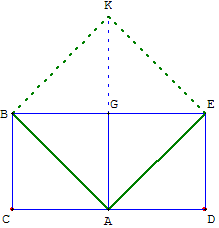
4.h. Carrés opposés par le sommet

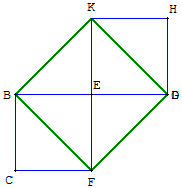
Construire deux carrés EBCF et EDHK, de côtés a et b,
aux côtés parallèles, ayant uniquement le sommet E en commun.

Une recherche, guidée par la figure de duplication du
carré ci-dessus, permet aux élèves, dans le cas
général, de trouver une solution en construisant un
carré à partir de [BK] ou de [FD].

Retrouver cette configuration dans : carrés du BOA,

similitude au bac

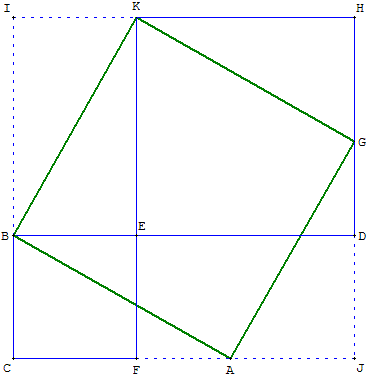
Carré ABKG solution, construit à partir du segment [BK].

On retrouve la figure de la démonstration de Pythagore des quatre triangles.

4.i. Puzzle de Gougu

Chine : puzzle reconstitué d'après Liu Hui,
époque Han, III^e siècle

Translation hors programme 

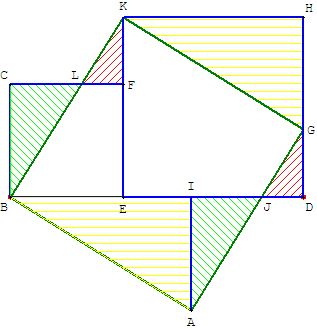
Puzzle de cinq pièces permettant de démontrer le
théorème de Pythagore en déplaçant trois pièces.

Par translation de trois triangles parallèlement aux
diagonales du grand carré, on passe de deux carrés
contigus au grand carré d'aire égale à la somme
des aires de deux petits carrés.

Ce puzzle est une des preuves du théorème de Pythagore.

5. Multiplication par 3 de l'aire d'un carré

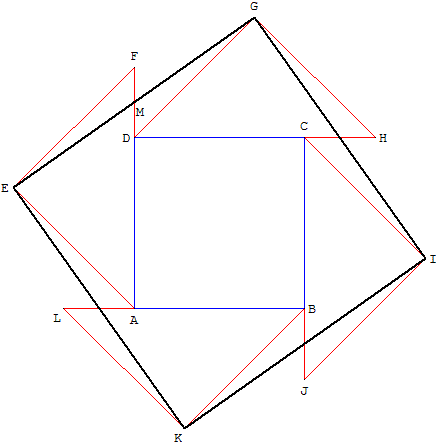
Construction d'Abu l-Wafa

Figure d'olivierl2 dans GeoGebraTube :
    trisection du carré par Abu'l Wafa

Voir aussi :
problème d'Abul-Wafa - Triangle équilatéral à l'intérieur d'un carré

Réciproque : trisection du carré si b = a

Abu'l-Wafa (Abul Wafa) est un mathématicien et astronome persan.

Autour d'un carré ABCD de côté a, on place quatre
triangles isocèles identiques de telle façon que le
sommet d'un des deux angles de 45° de chaque
triangle tombe sur un des sommets du carré ABCD
et l'hypoténuse le long du côté du carré.

En joignant les sommets des angles droits des triangles
rectangles, on obtient un carré EGIK.

On montre facilement que EGIK est un carré.

On montre ensuite que chacun des quatre triangles,
dépassant du carré EGIK, est égal à un triangle
manquant à l'intérieur du carré.

Par exemple, EDGF est un parallélogramme,
car (EF)//(DG) et EF = DG.
Le point M d'intersection de [EG] et de [DF] est le milieu de ces diagonales.

Le triangle excédent EMF est symétrique, par rapport
à M, du triangle manquant GMD. Leurs aires sont égales.

Le carré EGIK a une aire égale à l'aire de ABCD et
quatre fois l'aire du triangle rectangle AFE.

Lorsque AE = AD = a, le triangle ABCD a une aire triple du carré ABCD.

Si a est le côté de ABCD et b est la longueur des petits
côtés des triangles rectangles isocèles ;
AE = DG = CI = BK = b ; le carré EGIK a une aire égale
à a² + 2b².
Le carré EGIK a alors une aire égale à l'aire d'un carré
de côté a et de deux carrés de côtés b.

Voir : la trisection du carré de Christian Blanvillain

6.a. Triangle rectangle de petits côtés 1 et 2

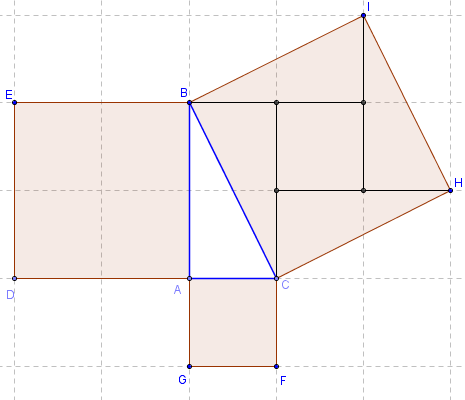
Figure du moulin à vent d'Euclide dans un quadrillage.

Le carré BCHI et formé du petit carré central et de
quatre triangles rectangles isométriques à ABC d'aires 1.

Son aire totale est de 5 et on retrouve le calcul
de la longueur de l'hypoténuse BC, qui mesure .

Figure GeoGebraTube :
    moulin à vent d'Euclide dans un quadrillage

Retrouver ce tracé dans la page : la planche à clous

6.b. Puzzle : reconstituer un carré avec 5 carrés alignés

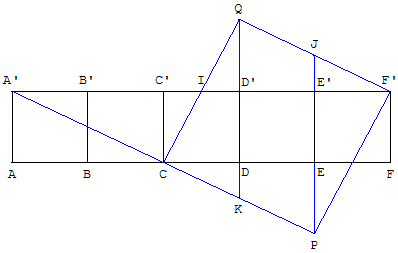
On aligne cinq carrés égaux consécutifs.

Reconstituer un carré.

6.c. Autres carrés à l'intérieur d'un carré

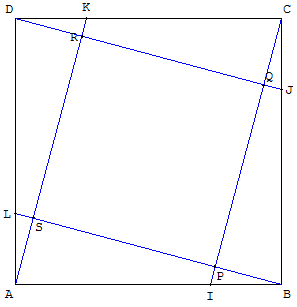
Sur les côtés d'un carré ABCD placer quatre points
I, J, K et L tels que : AI = BJ = CK = DL.

La droite (IC) est perpendiculaire à (LB).

PQRS est un carré.

Les carrés ABCD et PQRS ont même centre, centre de
la rotation, d'angle 90°, qui rend la figure invariante.

6.d. Quatre carrés à l'intérieur d'un carré

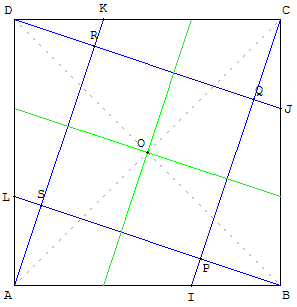
Cas particulier

Sur les côtés d'un carré ABCD placer quatre points
I, J, K et L tels que : AI = BJ = CK = DL = AB

PQRS est un carré,
Son aire est égale à de l'aire de ABCD.

Les médiatrices des côtés de PQRS rencontrent les côtés
de ABCDà leur tiers (les intersections de la médiatrice
de [SP] avec les côtés [AB] et [CD] sont les milieux de
[AI] et de [KC].
De même on a les milieux de [BJ] et [DL].)

7. Les trois carrés accolés

On aligne sur les figures ci-dessous trois carrés contigus égaux.

7.a. Somme de deux angles

Quelle est la somme des deux angles marqués x et y ?

La somme des deux angles vaut 45°.

Cinq méthodes pour le démontrer :

Calculs trigonométriques au lycée

7.a.1. En choisissant comme unité le côté d'un carré,
vérifier que AE = ; cos x = ; sin x = ;
BE = ; cos y = ; sin y = et la formule d'addition :

cos(x+y) = cos x cos y − sin x sin y

permettent de trouver cos(x+y) = , d'où x+y = 45°.

7.a.2. Pour amateurs de trigonométrie plus chevronnés,
remarquer que tan x = , tan y = .
Avec la formule tan(x+y) =
il vient : tan(x+y) = 1, et donc toujours x+y = 45°.

7.a.3. Le triangle ABC est triangle rectangle isocèle

La rotation de centre B d'angle 90° transforme le triangle
rectangle BEC en BFA, C a pour image A, d'où l'angle
CBA mesure 90°.
[BC] a pour image [BA], donc BC = BA.
L'angle aigu BÂC du triangle rectangle isocèle, égal à
la somme x + y, vaut 45°.

7.a.4. La réciproque de la propriété de Pythagore permet de le vérifier.

En choisissant comme unité le côté d'un carré,
ceux du triangle ABC ont pour longueurs :
AB = , BC = et AC = .
ABC est un triangle rectangle isocèle en B.

La somme x + y, égale à la mesure de l'angle aigu BÂC, vaut donc 45°.

7.a.5. Triangles rectangles semblables

En choisissant comme unité le côté d'un carré,
on a : DE = 1 et BD = 2, dans le triangle rectangle
BDE on a : tan y = DE/DB = .

Soit P le symétrique de C par rapport à F et Q, le
symétrique de G par rapport à B, APQE est un rectangle.
Sa largeur est PE = et sa longueur PA = 2.

Dans le triangle rectangle APE, tan(EÂP) = PE/PA = .
Les triangles rectangles BDE et APE sont semblables :
y = EÂP.

La somme x + y, égale à l'angle DÂP, vaut donc 45°.

7.b. L'embarras du choix

Pour montrer que les deux angles marqués x et z sont
égaux, utiliser une des quatre autres méthodes suivantes :

7.b.1. Calculs géométriques faisant intervenir des sommes d'angles

Avec y = DÂF, on a x + y = x + DÂF = 45°, somme trouvée en a.3 ci-dessus.
On a y + z = DÂF + FÂG = DÂG = 45°.
Soit x + y = y + z et en simplifiant par y : x = z.

Classe de seconde ou première

7.b.2. Calculer cos(x + 45°) dans le triangle AHF.

7.b.3. Calculer cos x avec Al-Kashi dans le triangle AGF.

7.b.4. Utiliser la loi des sinus : HF/sin x =… dans le triangle AHF.

7.c. Prouver un alignement

Classes de troisième - seconde

J est le milieu de [AG].
Montrer que les points C, I et J sont alignés.

Pour cela, trouver la position du point I sur [BG] et dire ce que
représentent le point I et la droite (CJ) dans le triangle ACG.

8. Huit carrés - Somme de trois angles

On aligne comme sur la figure ci-dessous huit carrés égaux.
Quelle est la somme des trois angles marqués x, y et z ?

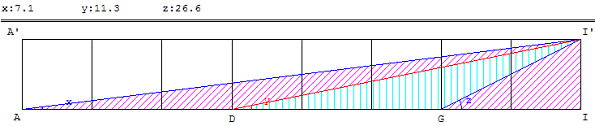
 La somme des trois angles vaut 45°.

Classe de 5^e, voir : un triangle dans un rectangle

Table des matières

Carré et deux triangles équilatéraux - Alignement de trois points

Le carré dans la planche à clous

Carrés et rotation

Orthocentre d'un triangle inscrit dans un carré

Aire d'un polygone formé par l'intersection de deux carrés

Le carré avec la géométrie dynamique

Multiplication par 5 de l'aire d'un carré

Carré dont les côtés passent par quatre points

Découpage d'aires dans un carré : exercices de-ci, de-là

Composer deux carrés avec quatre quadrilatères égaux : puzzle de Périgal

Droites perpendiculaires dans un carré : utiliser un orthocentre

Problèmes de partage

Aire minimale de deux carrés dans un carré

Lieux géométriques :
    – le carré mobile

    – le carré variable

Calculs d'angles dans un carré en 1^ère S : produit scalaire

Problèmes d'inscription

Carré inscrit dans un triangle

Trois carrés autour de BOA inscrits dans un triangle :
    voir problème de Grèbe

Carré inscrit dans un demi-cercle

Carré inscrit dans un quadrilatère

Sangaku : cercle et carré

Triangle inscrit dans un carré

Triangle équilatéral à l'intérieur d'un carré

Triangle équilatéral inscrit dans un carré

aire maximale

Google friendly,
sur ordinateur, cette page pour grand écran

La première page de ce document n'est pas une image
et une copie ne devrait pas être référencée comme telle par Google !

Copie twitter : t.co/EFetoHhcRz

Copyright 2007 - © Patrice Debart