Descartes et les Mathématiques

Homothétie

Démonstrations de géométrie utilisant l'homothétie ;
alignements, points de concours.

L'homothétie n'est plus étudiée en classe de première.

Sommaire

1. Transformé d'un triangle par homothétie

2. Configuration de base des homothéties

3. Parallélogramme et diagonale

      Parallélogramme de Pappus

4. Carré inscrit dans un triangle

5. Demi-cercle et carré

6. Prouver un point de concours

7. Triangle à côtés perpendiculaires

8. Homothéties transformant deux cercles
      Tangentes communes à deux cercles

9. Cercle tangent à deux droites passant par un point donné

10. Homothétie, triangle et centre de gravité

0. Définition

Une homothétie est une application ponctuelle caractérisée un centre O, point invariant, appelé centre et un réel k appelé rapport.
Par l'homothétie de centre O et de rapport k, le point M est transformé en un point M’ tel que ’ = .

L'homothétie laisse le centre O fixe et le transformé M’ est situé sur la droite (OM) par un agrandissement (si |k|>1) ou une réduction de rapport k.

1. Transformé d'un triangle par homothétie

Homothétie qui transforme un triangle en un autre triangle

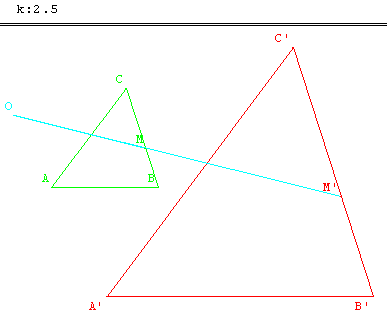
Le point M varie sur un triangle ABC.

h est une homothétie de centre O et de rapport k.

A’, B’, C’ et M’ les images respectives par h de A, B, C et M.

Télécharger la figure GéoPlan trihomo.g2w

2. Configuration de base des homothéties

Montrer un alignement

[AB], [CD] et [EF] sont trois segments parallèles distincts.

Monter que l es points I, J et K, placés selon la figure, sont alors alignés.

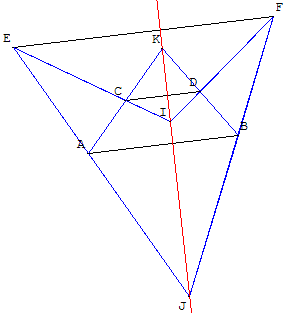
Indications

Il existe une homothétie f de centre K qui transforme le segment [AB] en [CD],
et une homothétie g de centre I qui transforme le segment [CD] en [EF].

Par g le point K a pour image K’, K et son transformé K’ sont alignés avec le centre I, I est situé sur la droite (KK’).

La composée h = gοf est une homothétie qui transforme le segment [AB] en [EF], son centre est le point J.

Par h le point K a pour image gοf (K) = g(K) = K’, K et K’ sont alignés avec le centre J, J est situé sur la droite (KK’).

Les points I et J, situés sur la droite (KK’), sont alignés avec K.

3. Parallélogramme et diagonale

3.a. Droites parallèles

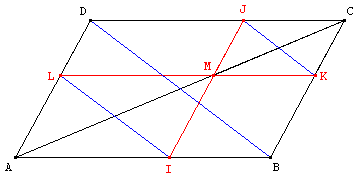
ABCD est un parallélogramme. M est un point variable sur la diagonale [AC].
Les droites issues de M parallèles à (BC) et à (AB) déterminent les points I, J, K et L.

En utilisant deux homothéties de centre A et C, montrer que les droites (IL), (BD) et (JK) sont parallèles.

Les parallélogrammes complémentaires ALMI et MJCK sont dits équivalents (Legendre – Éléments de géométrie – 1794).

3.b. Problème réciproque

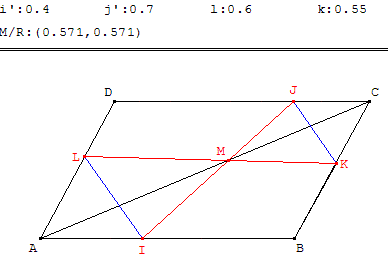
I, J et L sont trois points situés respectivement sur les côtés [AB], [CD] et [AD] d'un parallélogramme ABCD, distincts des sommets.

La parallèle à (IL), passant par J, rencontre (BC) en K.
Montrer que les droites (AC), (IJ) et (KL) sont concourantes.

Solution par la géométrie analytique

Pour cela, on considère le repère (A, , ) et on note i et j les abscisses de I et J, l et k les ordonnées de L et K.

Coordonnées des points de la figure : I(i, 0) ; J(j, 1) ; L(0, l) ; K(1, k).
Coordonnées de vecteurs : (−i, l) ; (1−j, k−1) ; (j−i, 1) ; (1, k−l)

Les vecteurs et étant colinéaires on a : i (1 − k) = l (1 − j).

Soit M, le point d'intersection des deux droites (AC) et (IJ) :

La droite (AC) a pour équation y = x.
Une équation de la droite (IJ), de vecteur directeur (j − i, 1), est y = (x − i).
Ces deux droites étant sécantes, en résolvant le système formé par ces deux équations, on trouve que les coordonnées de leur point M d'intersection sont :
x_M = y_M = .

Les coordonnées (x_M, y_M) de M vérifient l'équation de la droite (LK) :

La droite (LK), de vecteur directeur (1, k−l), a pour équation y − l = (k − l)x.

En substituant x_M et y_M dans cette équation on obtient : − l = (k − l) ,
soit i − l (i − j + 1) = (k−l)i, d'où i − ki = l − lj.

Cette égalité est vérifiée en raison de la colinéarité de et , donc les coordonnées de M vérifient l'équation y_M – l = (k – l)x_M.
Le point M est bien sur la droite (LK).

Les droites (AC), (IJ) et (KL) sont concourantes en M.

3.c. Parallélogramme de Pappus

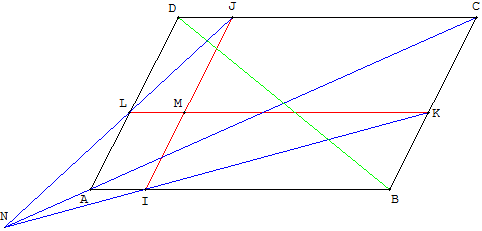
M est un point variable du plan n'appartenant pas à la diagonale (BD).
La parallèle à (AD) passant par M coupe (AB) en I et (CD) en J.
La parallèle à (AB) passant par M coupe (BC) en K et (AD) en L.

Les droites (IK) et (JL) sont sécantes en un point N, les points A, C et N sont alignés.

Œuvres de Pappus :

Théorème de Pappus : plan projectif

Petit théorème de Pappus

Démonstration par Pappus du théorème de Pythagore

Cette figure permet aussi de proposer, en classe de 3^e, le problème assez difficile suivant :
Si M est un point variable sur la diagonale [AC], montrer que les aires des parallélogrammes IBKM et LMJD sont égales.
Voir : deux parallélogrammes d'aires égales

Indications

On note P l'intersection de (IK) et (CD) et Q l'intersection de (LJ) et (BC).
Montrer que les droites (IL) et (PQ) sont parallèles (théorème de Pappus, preuve analytique ci-dessous).

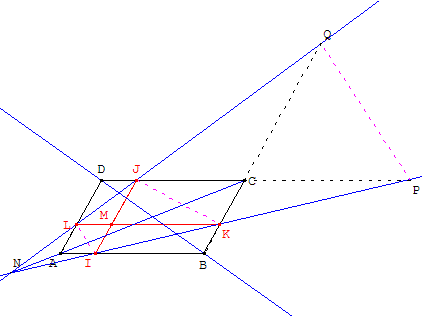
L'homothétie h de centre N, qui transforme I en P, transforme (IL) en sa parallèle (PQ), donc transforme L en Q.
h transforme la droite (AB), passant par I, en sa parallèle passant par P, donc en (CD).
De même, h transforme (AD), passant par L, en sa parallèle passant par Q, donc en (BC).
h transforme donc (AB) et (AD) en (CD) et (BC). h transforme le point d'intersection A des deux premiers côtés en C point d'intersection des deux autres.
Le centre d'homothétie N est aligné avec le point A et son image C : les points N, A et C sont alignés.

Classe de 2^nde

Dans le repère (A, , ), il est facile et élégant de faire une démonstration en géométrie analytique.

Si les coordonnées de M sont (a, b), celles des points d'intersection avec le parallélogramme sont : I(a, 0); J(a, 1) ; L(0, b) et K(1, b).
Les coordonnées des vecteurs directeurs (1 –a, b) et (a, 1 – b) permettent de trouver les équations des droites (IK) et (LJ) :
bx + (a – 1)y = ab,
(b – 1)x + ay = ab.

En calculant la différence de ces deux équations et en substituant on obtient :
x – y = 0,
x = ab/(a + b – 1).

Le point N est bien sur la diagonale (AC) d'équation x – y = 0,
à condition que M ne soit pas sur l'autre diagonale (BD) d'équation x + y – 1 = 0.

Remarque : démonstration de (IL) // (PQ).
(–a, b) : la droite (IL), d'équation bx + ay = ab, a coefficient directeur – b/a.
Les coordonnées de P et Q sont P(1, (ab + 1 – a)/b) et Q((ab + 1 – b)/a), 1) ; d'où ((ab + 1 – a – b)/b, (ab + 1 – a – b)/a).
La droite (PQ) a aussi pour coefficient directeur – b/a et est parallèle à (IL).

4. Carré inscrit dans un triangle

Soit ABC un triangle. Trouver un carré DEFG inscrit dans le triangle ABC : ses sommets sont sur les côtés du triangle ; deux des sommets du carré sont sur [AB], un troisième sur [AC] et le quatrième sur [BC]).

4.a. Construction avec une homothétie

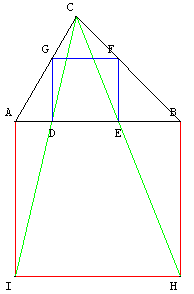
Tracé avec une homothétie de centre C

Construire un carré de côté [AB] et utiliser une homothétie de centre C pour trouver le côté [DE] du carré solution.

Figure interactive dans GeoGebraTube : carré inscrit dans un triangle

Cas particulier : carré inscrit dans un triangle rectangle

Trois carrés inscrits dans un triangle : voir problème de Grèbe

Carré d'aire maximale, voir : olympiades Versailles 2005

4.b. Problème BOA

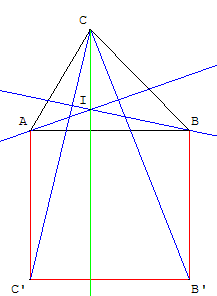
Les perpendiculaires à (CB’) issue de A et à (CC’) issue de B se coupent en I.
La droite (CI) semble perpendiculaire à la droite (AB) ?

Démonstration par les rotations :
voir figure de Vecten dans carrés autour de BOA

      ou figure du « moulin à vent » d'Euclide

4.c. Homothétie de centre A

Classe de cinquième

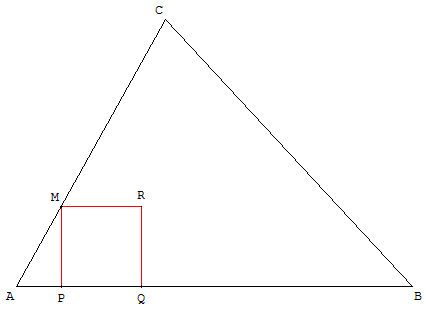
Placer un point M sur le côté [AC] du triangle.

Soit P la projection orthogonale de M sur la droite (AB).
Construire le carré direct MPQR de côté [MP], son deuxième côté [PQ] se trouve sur la droite (AB).

Avec GéoPlan, on peut chercher une solution en déplaçant le point M.

Construction

Tracer un carré MPQR quelconque dont deux des sommets sont sur [AB] et un sur [AC]. Joindre A au quatrième sommet de ce carré et prolonger la droite (AR) jusqu'à ce qu'elle rencontre [BC]. Le point d'intersection F sera un sommet du carré recherché.
Il suffit de tracer à partir de F la parallèle et la perpendiculaire à [AB] pour compléter le tracé du carré.

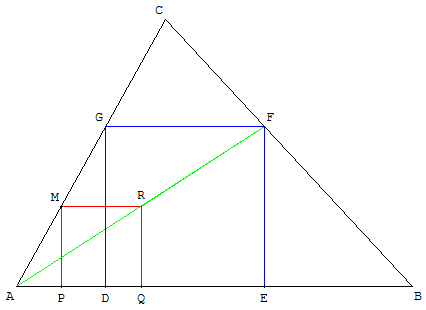
Preuve

La droite (AR) rencontre la droite (BC) en F.
L'homothétie de centre A qui transforme R en F transforme le carré MPQR en un carré GDEF dont les sommets sont sur les côtés du triangle ABC.

Voir : la géométrie à l'épreuve pratique de terminale S avec GéoPlan et GéoSpace.

5. Carré inscrit dans un demi-cercle

L'École d'Athènes - Raphaël, vers 1510 - Musée du Vatican

5.a. Carré inscrit entre un demi-cercle et son diamètre

Classe de première L

Construire un carré de côté [AB] et utiliser une homothétie de centre O milieu de [AB].

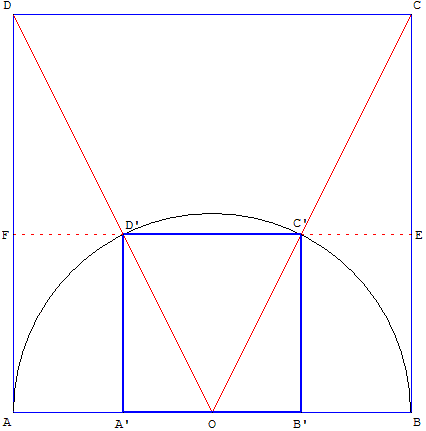
Longueur du côté d'un carré inscrit dans un demi-cercle :
A’B’ = AB/ ;
le côté du carré A’B’C’D’ est égal au diamètre AB, divisé par .

En effet, si le côté du carré est 1, alors OA’ = et A’D’ = 1,
l'hypoténuse OD’ du triangle rectangle OA’D’ mesure et est égale au rayon du cercle.
AB’ = AO + OB’ = + = est égal au nombre d'or φ.

ABEF est un « rectangle » : le rapport entre la longueur et la largeur est . Il est la juxtaposition d'un carré de côté 1 et deux rectangles d'or de longueur 1 et de largeur

AB’C’F et A’BED’ sont des rectangles d'or de longueur φ et de largeur 1.

Voir tracé régulateur

Construction du pentagone à partir d'un carré inscrit dans un demi-cercle

5.b. Construction du carré dans un demi-cercle

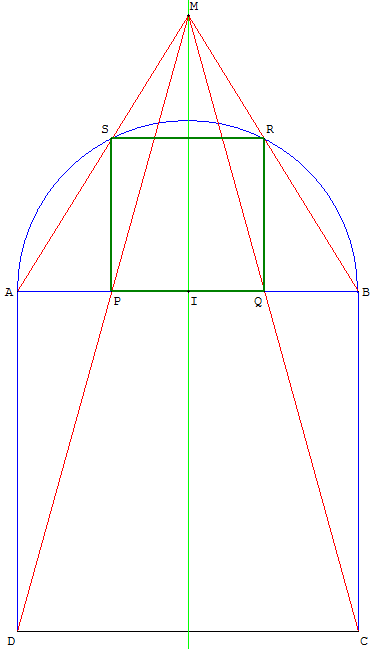
À partir d'une autre homothétie

Une deuxième homothétie de rapport transforme le carré ABCD en SRQP, carré de sommets P et Q situés sur [AB], inscrit dans le demi-cercle de diamètre [AB], à l'extérieur de ABCD.

En étudiant les triangles semblables de la figure, on trouve que le centre M d'homothétie, situé sur la médiatrice de [AB], est tel que IM = AB × .

Variante
On construit un rectangle MNPQ inscrit à l'intérieur d'un demi-cercle de diamètre [AB]: M et N sur [AB] ; P et Q sur le demi-cercle.

Quelles sont les positions pour lesquelles la longueur du rectangle est le double de la largeur ?
    Pour lesquelles la longueur est égale à quatre fois la largeur ?

6. Prouver un point de concours

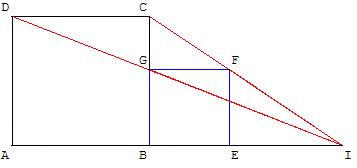
Deux carrés ABCD et BEFG ont un sommet commun B et deux côtés alignés :
E est sur la droite (AB) ; G est sur la droite (BC).

Montrer que les droites (AB), (DG) et (CF) sont concourantes.

7. Triangle à côtés perpendiculaires

Problème de construction

Construire un triangle MNP inscrit dans un triangle ABC ayant ses « côtés perpendiculaires » à ceux du triangle ABC.

figure GéoPlan tria_cote_perpendiculaire_3.g2w

Analyse

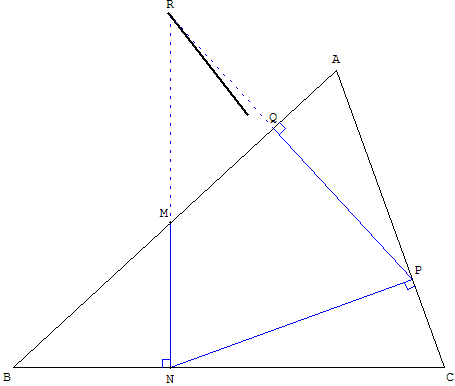
Soit un point M de [AB]. On appelle N le projeté orthogonal de M sur (BC), P le projeté orthogonal de N sur (AC), Q le projeté orthogonal de P sur (AB).

En général, la ligne brisée MNPQ ne se referme pas et on appelle R le point d'intersection des droites (MN) et (PQ).

Géométrie dynamique

Déplacer le point M. On trouve une solution lorsque les points M et Q sont confondus avec le point R.

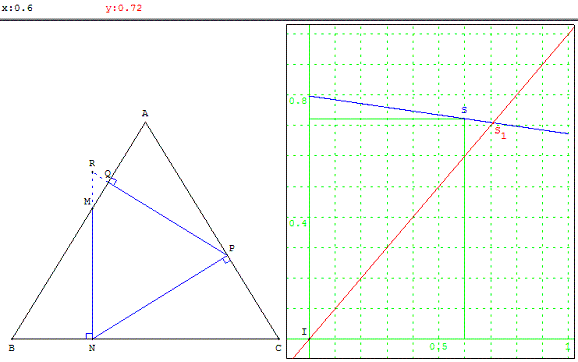
Le problème admet une solution : figure ci-dessus

Soit x l'abscisse du M dans le repère (B, ) et y l'abscisse de Q.

La fonction qui à x fait correspondre y est une fonction affine décroissante de l'intervalle [0, 1].
Il existe donc dans le graphique un point S₁ où la droite représentative de cette fonction coupe la droite d'équation y = x.

Construction géométrique de la solution : figure ci-contre à droite.

La trace du point R est une droite passant par C permettant de mettre en évidence des homothéties de centre C.

figure GéoPlan tria_cote_perpendiculaire.g2w

Utilisation des propriétés de l'homothétie

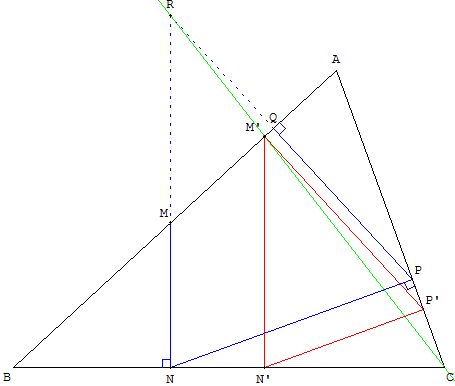
Synthèse

La droite (CR) rencontre (AB) en M’. L'homothétie de centre C qui transforme R en M’ transforme N en N’ et P en P’. Le triangle M’N’P’ a ses côtés parallèles aux côtés de RNP, donc orthogonaux aux côtés du triangle ABC.
Le triangle M’N’P’ inscrit dans ABC est une solution.

Une deuxième solution

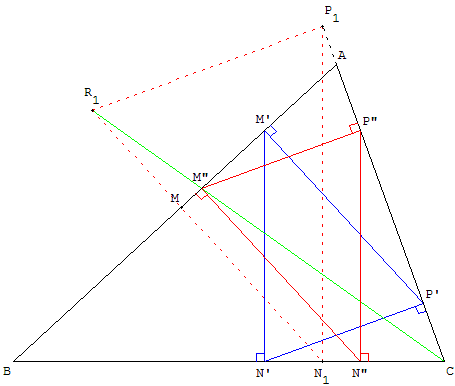
En plaçant le point N₁ sur la perpendiculaire à (AB) en M, on construit le triangle N₁P₁>R₁. La droite (CR₁) rencontre (AB) en M”. L'homothétie de centre C qui transforme R₁ en M” permet de construire une deuxième solution : le triangle M”N”P”.

figure GéoPlan tria_cote_perpendiculaire_2.g2w

Problèmes de contact

8. Homothéties transformant deux cercles

Tangentes communes à deux cercles

Soit deux cercles c(O, r) et c’(O’, r’) tel que r < r’,
le petit cercle (c) n'est pas à l'intérieur de (c’) : r + OO’ > r’.

8.a. Cercles d'un même côté des tangentes

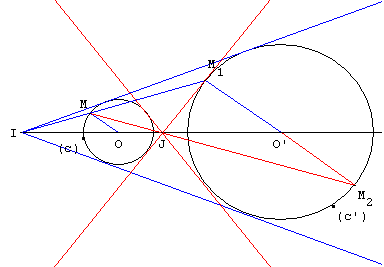
8.b. Quatre tangentes pour deux cercles non sécants

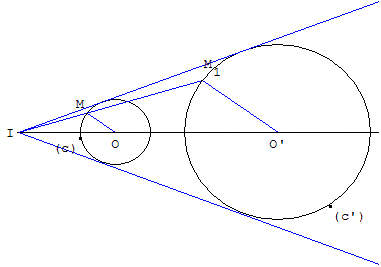
Il existe une homothétie de rapport positif r’/r transformant (c) en (c’). Le centre I de cette homothétie est situé sur la ligne des centres (OO’).
Pour le trouver, il suffit, étant donné un point M variable sur (c), de tracer un rayon OM₁ parallèle à OM et de même sens. Le point M₁ de (c’) est alors l'image de M par l'homothétie et ces points sont alignés avec I. Le point I est l'intersection des droites (OO’) et (MM₁).

Par I on peut mener deux tangentes communes aux deux cercles.
Les points de contact se tracent avec précision, par exemple, comme points d'intersection du cercle (c) avec le cercle de diamètre [IO].

De même, on trouve le centre J de l'homothétie de rapport négatif −r’/r, transformant (c) en (c’), en traçant le point M₂ de (c’), tel que le rayon OM₂ soit parallèle à OM et de sens contraire.
Si les cercles (c) et (c’) sont extérieurs l'un à l'autre (r + r’ < OO’), J est alors le point de concours de deux autres tangentes.
Dans ce cas, on trouve les points de contact comme intersection du cercle (c) avec le cercle de diamètre [OJ] ou comme intersection du cercle (c’) avec le cercle de diamètre [JO’].

Étudier les cas particuliers où les cercles ont le même rayon : il existe deux tangentes communes parallèles à la ligne des centres.

En conclusion si un des cercles est l'intérieur de l'autre, pas de tangente commune.
Si les cercles sont tangents intérieurement, la tangente au point de contact est la seule tangente commune.
Si les cercles sont sécants en deux points, il y a deux tangentes communes.
Si les cercles sont tangents extérieurement, il y a trois tangentes communes, en comptant la tangente au point de contact.
Si les cercles sont extérieurs l'un à l'autre, il y a quatre tangentes communes.

Voir l'adaptation au collège de cet article dans : constructions en troisième

        les constructions avec deux cercles auxiliaires : le cercle au collège

Application
Trouver les centres d'homothétie de deux cercles

Tracer les diamètres perpendiculaires à la ligne des centres.

Lorsqu'elles existent, les droites passant par les extrémités des diamètres rencontrent la ligne des centres aux centres d'homothétie.

8.c. Axe radical

Notion disparue de l'enseignement français au lycée.

L'axe radical de deux cercles, de centres distincts, est l'ensemble des points qui ont même puissance par rapport à ces deux cercles.
L'axe radical est une droite perpendiculaire à la ligne des centres.
Les tangentes menées aux deux cercles à partir d'un point de l'axe radical (extérieur aux deux cercles) ont même longueur.

Voir géométrie du cercle

        Inversions échangeant deux cercles

8.d. Tangentes aux points de contact

Soit I le point d'intersection des tangentes extérieures à deux cercles extérieurs. Par I, on trace une droite qui coupe les deux cercles en quatre points. Les tangentes en ces quatre points forment un quadrilatère.
Montrer que :
    8.d. a. ce quadrilatère est un parallélogramme,
    8.d. b. une de ses diagonales passe par I,
    8.d. c. l'autre diagonale est l'axe radical des deux cercles.

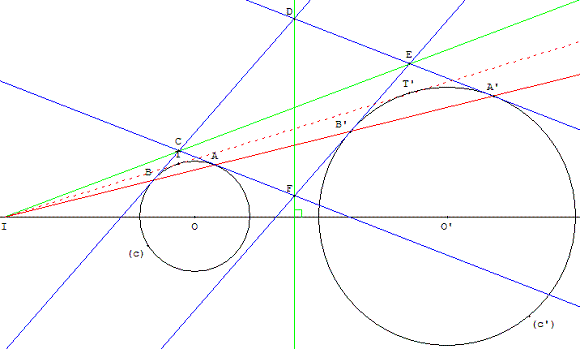
Le point I existe si les cercles (c) et (c’) sont de rayons différents, il est alors le centre d'homothétie positive de ces deux cercles.

8.d. a. La sécante menée par I coupe (c) en A et B et (c’) en ses images A’ et B’.
Les tangentes en A’ et B’ à (c’) sont les images des tangentes à (c) en A et B.
Nous avons donc deux couples de droites parallèles qui forment un parallélogramme CDEF, à condition que la sécante ne soit pas confondue avec la ligne des centres (OO’).

8.d. b. Les tangentes en A et B se coupent en C, les droites images, tangentes en A’ et B’ au cercle (c’), se coupent en E.
Les points C et E sont homologues par l'homothétie et sont donc alignés avec son centre I.

8.d. c. Les triangles BAC et BA’D, ayant leurs côtés deux à deux parallèles ou confondus, sont homothétiques.
Le premier étant isocèle, car CA = CB, le deuxième l'est aussi : DA’ = DB, le point D a même puissance par rapport aux deux cercles.
À l'aide des triangles B’AF et B’A’E on procède de même pour prouver que le point F a même puissance par rapport aux deux cercles.
La droite (DF) est l'axe radical des deux cercles.

9. Cercle tangent à deux droites, passant par un point donné

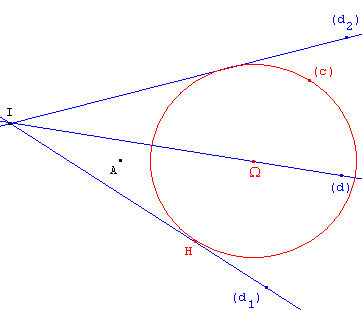
On donne deux droites (d₁), (d₂) sécantes et un point A n'appartenant pas à ces droites.
Existe-t-il un cercle (c) passant par A tangent à ces deux droites ?
Combien y a-t-il de solutions à ce problème ?

Analyse

Placer un point variable Ω sur la bissectrice de (d₁, d₂) située dans le même secteur angulaire que A et tracer le cercle (c), passant par H projection orthogonale de Ω sur la droite (d₁). Ce cercle est tangent aux deux droites.
Avec un logiciel de géométrie dynamique, il suffit de déplacer Ω pour trouver deux solutions.

Construction de Wallis basée sur la puissance d'un point par rapport à un cercle :

voir problème de contact PDD

Solution avec un cercle auxiliaire

Utiliser des homothéties, de centre I, transformant le cercle (c) en des cercles passant par A.

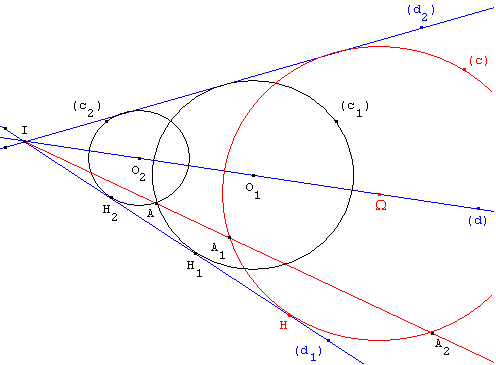
Étant donné un cercle (c), la droite (IA) rencontre (c) en deux points A₁ et A₂.
L'homothétie de centre I qui transforme A₁ en A, transforme Ω en O₁, H en H₁ et le cercle (c) en (c₁),
l'autre homothétie de centre I qui transforme A₂ en A, transforme Ω en O₂, H en H₂ et le cercle (c) en (c₂).

Les cercles (c₁) et (c₂), passant par A, tangents à (d₁) et (d₂), sont les deux solutions du problème.

10. Homothétie, triangle et centre de gravité

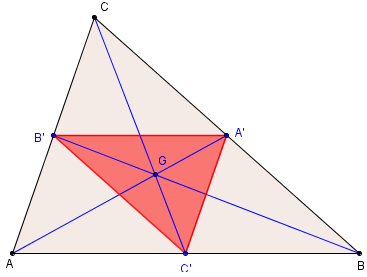
ABC est un triangle;
A’, B’ et C’ sont les milieux des côtés [BC], [CA] et [AB] ;
G est son centre de gravité.

Les points A, B et C sont les images de A’, B’ et C’ par l'homothétie h de centre G et de rapport −2.

Le triangle A’B’C’, dont les sommets sont les pieds des médianes, est le triangle médian du triangle ABC.
Le triangle médian est l'homothétique du triangle ABC, par l'homothétie réciproque h^{– 1} de centre G et de rapport .

Les droites des milieux partagent le grand triangle en quatre triangles homothétiques : dans le rapport pour le triangle médian, dans le rapport pour les trois autres.

Figure interactive dans GeoGebraTube : triangle médian

Exercice 10.a.

Soit P, Q et R les symétriques d'un point M du plan par rapport aux milieux A’, B’ et C’ des côtés d'un triangle ABC.

Montrer que les segments [AP], [BQ] et [CR] ont même milieu.

Solution : composée d'homothéties

La composée de l'homothétie f de centre M et de rapport , suivie l'homothétie h de centre G et de rapport − 2 a pour rapport k = × (−2) = − 1, c'est une symétrie centrale de centre I.

Le centre I est donc le milieu des segments [AP], [BQ] et [CR].

Exercice 10.b.

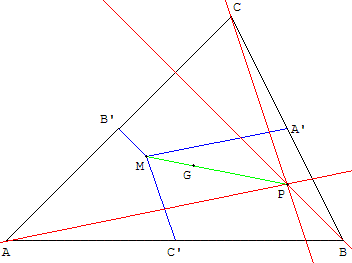
Soit ABC un triangle ; les points A’, B’ et C’ les milieux des côtés [BC], [CA] et [AB] ; G son centre de gravité.

Étant donné un point M du plan, montrer que la parallèle à (MA’), passant par A, la parallèle à (MB’), passant par B, et la parallèle à (MC’), passant par C, sont concourantes.

Solution

Le point P de concours est l'image de M par l'homothétie h de centre G et de rapport − 2.

L'homothétie h transforme (A, B, C) en (A’, B’, C’) et M en un point P.
Ce point P est sur l'image par h de (MA’), c'est-à-dire la parallèle passant par A à (A’M).
Pour les mêmes raisons, P est sur la parallèle à (B’M), passant par B, et est sur la parallèle à (C’M), passant par C.

Ces trois droites sont concourantes en P.

Table des matières

Index Transformations

Homothétie dans d'autres pages du site

Cordes de cercles tangents et point fixe : Angles - Rotations

Quadrilatère complet : le plan projectif

Les carrés autour de BOA

Euler : la géométrie du triangle

Parallélogramme et homothétie : partage en trois

Lieu du transformé d'un point mobile sur un cercle

Homothétie transformant deux paraboles,

      Homothétie transformant deux hyperboles

Téléchargement

Télécharger homothetie.pdf : ce document au format « .pdf »

Google friendly