Descartes et les Mathématiques
Géométrie du triangle III
Cercles remarquables
Théorème de Feuerbach, cercle et point d'Apollonius.
Sommaire
1. Théorème de Feuerbach
Le cercle d'Euler est tangent aux cercles inscrit et exinscrits
Points et triangle de Feuerbach
2. Milieux des segments joignant les centres des cercles inscrit et exinscrits
De jolies « babioles » des mathématiques de grand-papa,
qui font le bonheur des amateurs de la géométrie du triangle.
Pour le logiciel, ce ne sont que des calculs, assez complexes,
que l'on pourra bientôt écrire de façon automatique.
Bien que naguère négligée, la géométrie du triangle permet
aux mathématiciens professionnels de faire le trait d'union
entre le discret et le continu.
Ces géométries riches, enseignées en terminale jusqu'en 1960,
ont été sacrifiée au profit de l'algèbre linéaire
et des mathématiques discrètes, bien moins « s e x y ».
Mais quoi de plus formateur que de s'approprier une figure géométrique
et quelle joie lorsque l'on a fini de sécher sur un problème.
1. Théorème de Feuerbach
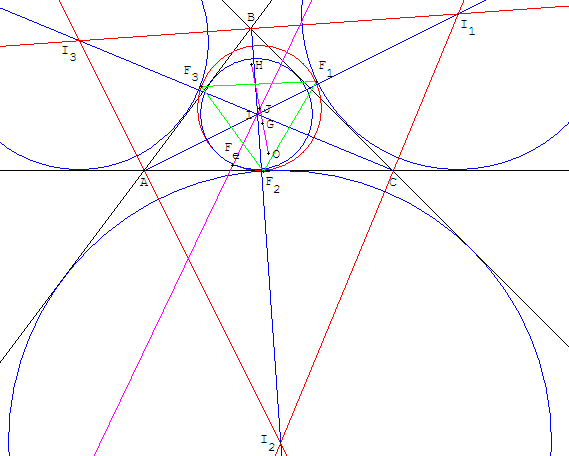
Théorème : dans un triangle, le cercle d'Euler est tangent
au cercle inscrit et aux trois cercles exinscrits.
Comme son nom l'indique, ce théorème a été découvert en 1822
par Feuerbach (1800-1834), puis démontré par M'Clelland en 1891
et Lachlan en 1893.
Les quatre points Fe, F1, F2 et F3 de contact
entre le cercle d'Euler et le cercle inscrit
et les trois cercles exinscrits s'appellent les points de Feuerbach du triangle.
Fe est le point X(11) dans ETC.
Les trois points F1, F2 et F3 de contact aux cercles exinscrits
forment le triangle de Feuerbach du triangle donné.
Le centre I du cercle inscrit dans le triangle
ABC est l'orthocentre du triangle I1I2I3
(acutangle : dont les trois angles sont aigus) formé
par les points d'intersection des trois bissectrices extérieures.
Ce triangle I1I2I3, formé par les bissectrices extérieures, de sommets
les centres des trois cercles exinscrits,
s'appelle le triangle de Bevan du triangle ABC.
Figure interactive dans GeoGebraTube : théorème de Feuerbach
1.2. Alignement du point de Feuerbach avec les centres
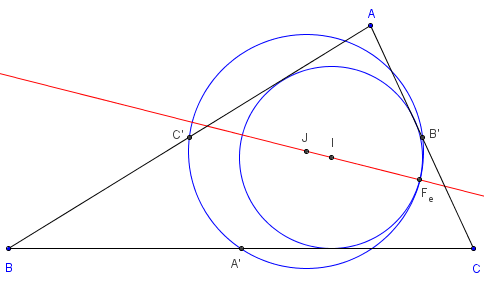
Le point de Feuerbach Fe, point de contact du cercle d'Euler
et du cercle inscrit,
est situé sur la droite des centres (IJ) ; I et J centres
des cercles inscrit et d'Euler.
Preuve : la tangente commune aux deux cercles en
Fe est perpendiculaire aux rayons IFe et JFe.
Figure interactive dans GeoGebraTube :
point de Feuerbach - Alignement avec les centres
Figure exportée dans WikiPédia : Points de Feuerbach
Un quatrième point sur la droite des centres (IJ)
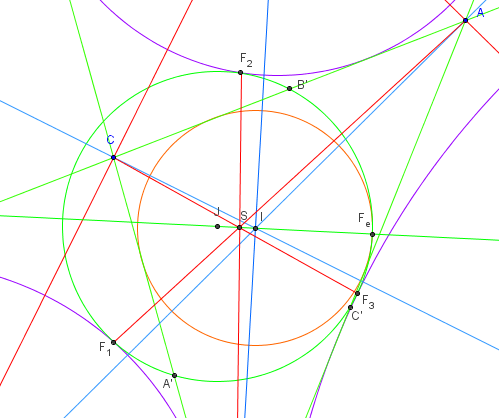
Soit S le point de concours des céviennes AF1, BF2 et CF3.
Alors le point S, le centre I du cercle inscrit, le centre J du cercle d'Euler
et le point de Feuerbach Fe sont alignés et en division harmonique.
Figure interactive dans GeoGebraTube :
point de Feuerbach - Alignement de 4 points
Trois autres droites concourantes au point de Feuerbach
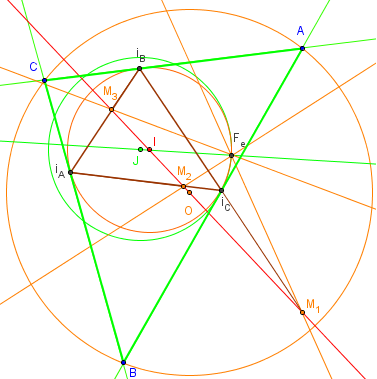
Soit O le centre du cercle circonscrit.
Les points de contact iA, iB, iC du cercle inscrit avec les
côtés du triangle ABC forme le triangle de contact iAiBiC.
Les trois droites symétriques de la droite (IO),
par rapport aux côtés du triangle de contact,
passent par le point de Feuerbach Fe.
Pour tracer la droite symétrique, placer le point double Mi
intersection de la droite (IO) et du côté, puis trouver le
symétrique d'un autre point, par exemple I.
Figure interactive dans GeoGebraTube :
droites concourantes au point de Feuerbach
1.3. Le point de Feuerbach
et les pieds des bissectrices sont cocycliques
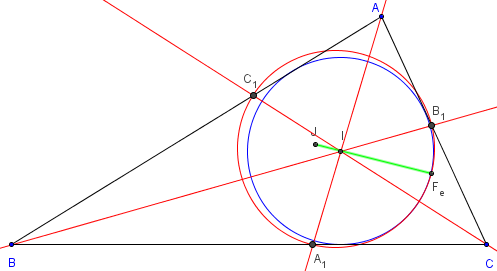
Les pieds A1, B1 et C1 des bissectrices intérieures du triangle ABC
forment le triangle pédal A1B1C1 du centre I du cercle inscrit.
Le cercle pédal, circonscrit au triangle pédal A1B1C1,
passe par le point de Feuerbach.
Figure interactive dans GeoGebraTube : point de Feuerbach et bissectrices
Cercles inscrits et théorème de Feuerbach dans le triangle rectangle
2. Milieux des segments joignant les
centres des cercles inscrit et exinscrits
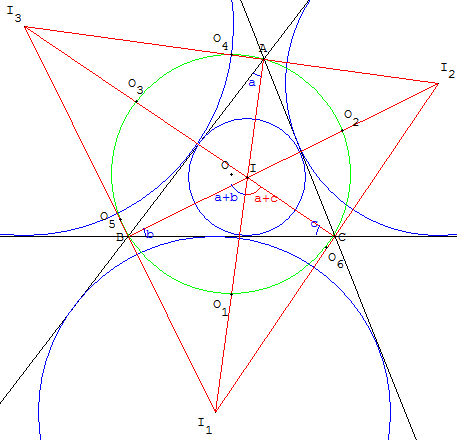
Les milieux des segments joignant les centres des cercles
inscrit et exinscrits sont sur le cercle circonscrit.
Application : construire un triangle connaissant ses trois bissectrices
avec les centres de cercles exinscrits
Dans un triangle ABC, tracer les bissectrices intérieures et extérieures.
Leurs points d'intersection sont les centres I, I1, I2, I3 des cercles inscrit
et exinscrits, tangents aux trois côtés du triangle.
On note O1 le milieu de [II1], situé sur la bissectrice intérieure (AI),
et les angles BAC = 2a, ABC = 2b et BCA = 2c.
I, centre du cercle inscrit, est à l'intersection
des bissectrices intérieures (BI) et (CI).
I1, centre d'un cercle exinscrit, est à l'intersection
des bissectrices extérieures (BI1) et (CI1).
Les bissectrices intérieures et extérieures sont perpendiculaires,
d'où les angles IBI1 et ICI1 sont droits. Le quadrilatère BICI1 est inscriptible
dans le cercle de diamètre [II1] de centre O1 passant par B et C.
Dans ce cercle, le double de l'angle inscrit II1C
est égal à l'angle au centre IO1C, angle égal à AO1C.
Le supplémentaire de la somme des angles aigus de IAC est l'angle :
I1IC = a + c.
Dans le triangle rectangle I1IC, l'angle II1C est le complémentaire de I1IC,
d'où II1C = 
– (a + c).
AO1C = IO1C = 2 II1C = 2 { – (a + c)} = 2b car la somme
2(a + b + c)
des angles du triangle ABC est égal à π.
On a donc AO1C = ABC, le point O1 est situé sur le cercle circonscrit.
Le milieu d'un segment joignant les centres de
deux cercles exinscrits est situé sur le cercle circonscrit.
On note O6 le milieu de [I1I2], situé sur la bissectrice extérieure
passant par C. Les points C, I1, I2 et O2 sont alignés sur cette bissectrice.
Comme précédemment, les angles I1AI2 et I1BI2 des bissectrices sont droits.
Le quadrilatère I1BAI2 est inscriptible dans le cercle de
diamètre [I1I2] de centre O6 passant par A et B.
Dans ce cercle, en considérant l'angle inscrit AI1I2
et son angle au centre AO6I2, on a AO6C = 2 AI1I2 = 2 { – (a + c)} = 2b.
On a donc AO6C = ABC, le point O6 est situé sur le cercle circonscrit.
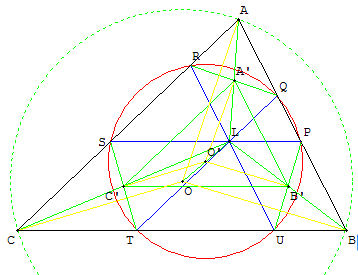
3. Cercle et point d'Apollonius
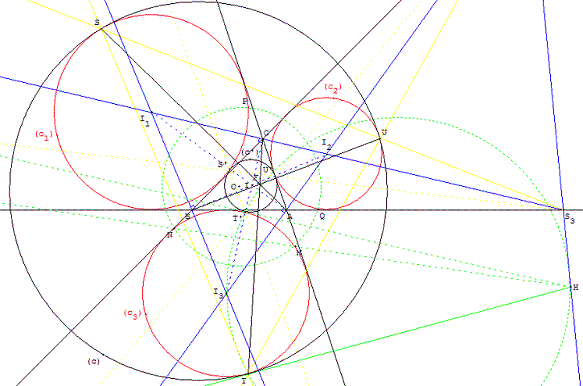
Dans un triangle, les droites joignant respectivement les sommets
aux trois points de contact du cercle d'Apollonius,
tangent intérieurement aux cercles exinscrits, sont concourantes.
Le point de concours est le point d'Apollonius (point X(181) dans ETC).
Construction
Dans un triangle ABC, tracer les bissectrices intérieures et extérieures.
Leurs points d'intersection extérieurs au triangle, situés à égale distance
des trois côtés du triangle, sont les centres I1, I2, I3 des cercles
exinscrits (c1), (c2), (c3), tangents aux trois côtés du triangle.
La construction des cercles tangents à trois cercles,
du problème d'Apollonius, permet de construire le cercle d'Apollonius (c) :
Soit S1, S2 et S3 les centres des homothéties positives échangeant
les trois cercles : S1 est l'intersection de (BC) et (I2I3),
S2 intersection
de (AC) et (I1I3) et S3 intersection de (AB) et (I1I2).
Étant donné un point M variable sur le cercle (c3) construisons
les points P intersection bien choisie de (c1)
avec (S2M) et Q intersection de (c2) avec (S1M).
Le cercle circonscrit au triangle MPQ recoupe (c3) en N.
La droite (MN) est l'axe radical de MPQ et de (c3).
Elle coupe la ligne (S1S2) des centres d'homothétie en H.
Le point H est indépendant du point M ; la puissance du point H
par rapport à (c3) est aussi celle par rapport au cercle cherché (c).
La tangente commune à (c) et (c3) passe par H.
Il suffit de trouver les points de tangence T et T’,
intersection de (c3) avec le cercle de diamètre [I3H].
En traçant le point U intersection de (c1) avec (S2T) et le point S
intersection de (c2) avec (S1T), on trouve le cercle (c) circonscrit à TUS.
De même, on trace U’ intersection de (c1)
avec (S2T’), et S’ intersection de (c2) avec (S1T’).
T’, U’ et S’ sont les points de Feuerbach du triangle. T’U’S’
est le triangle de Feuerbach du triangle ABC.
Le cercle (c’) circonscrit à T’U’S’ n'est autre que le cercle d'Euler tangent
aux trois cercles exinscrits. Ce résultat constitue le théorème de Feuerbach.
Les droites (AS), (BU) et (CT) sont concourantes au point d'Apollonius F.
Soit O le centre du cercle circonscrit au triangle ABC,
I le centre du cercle inscrit dans ABC, Ω’ le centre
du cercle (c’) d'Euler et Ω le centre du cercle (c).
Les droites (OI) et (ΩΩ’) sont parallèles et perpendiculaires
à la ligne des centres d'homothétie (S1S2). Les points O, I et F sont alignés.
À ne pas confondre avec le faisceau des cercles d'Apollonius d'un triangle
WikiPédia mobile: Problème des contacts
4. Cercles de Tücker
Définition 1 : homothétie
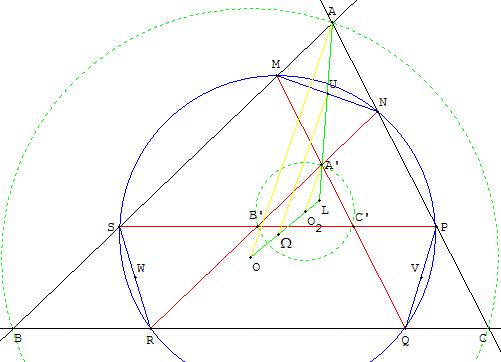
Dans une homothétie de centre L, le point de Lemoine, de rapport k
(k ≠ 1 et k ≠ 0), le triangle ABC a pour image A’B’C’.
Les côtés du triangle A’B’C’ rencontrent
ceux du triangle ABC en six points.
Ces points cocycliques sont situés sur un cercle (T)
dit de Tücker du triangle ABC.
Propriétés
Les milieux U, V, W des segments [MN], [PQ], [RS] sont situés sur
les symédianes et forment un triangle UVW homothétique
de ABC dans une homothétie de centre L.
Les droites (MN), (PQ) et (RS) sont antiparallèles aux côtés du triangle
et les segments qu'elles déterminent sont de même longueur.
Le centre Ω du cercle (T) est le milieu du segment [OO2] formé
par les centres des cercles circonscrits aux triangles ABC et A’B’C’.
Indications
Les milieux U, V, W des segments [MN], [PQ], [RS] sont situés
sur les symédianes, les segments sont antiparallèles aux côtés opposés.
Voir : milieu d'une antiparallèle
Les droites (MN, CB) sont antiparallèles aux droites (AB, CA) :
(AB, MN) = (CB, CA).
Les droites (SR, CA) sont aussi antiparallèles aux droites (BC, BA) :
(BA, SR) = (CA, CB).
On en déduit que (BA, SR) = − (AB, MN).
Comme (AB) //(NR) on a : (BA, SR) = − (NR, MN).
Avec les points de l'hexagone MNPQRS on a (SM, SR) = (NM, NR).
Les points S, M, N, R n'étant pas alignés, cette égalité d'angles
montre qu'ils sont cocycliques, situés sur un cercle (T).
Indications
De (BC)//(PS) et (MN) antiparallèle à (BC) on en déduit que (PS)
est antiparallèle à (MN) par rapport à (MS) et (PN). (PS, PN) = (MS, MN).
P, S, M, N sont cocycliques, P appartient au cercle circonscrit à S, M, N :
le cercle (T). On montre de même que (T) contient le point Q.
Construction d'une antiparallèle
ABC est un triangle de cercle circonscrit (Γ) de centre O.
Définition 2 : À partir d'un point M de (AB) distinct de A,
mener la droite antiparallèle de (BC) par rapport à (AB, AC).
C'est la parallèle à la tangente en A à (Γ), donc perpendiculaire à (AO).
Elle coupe (AC) en N. La parallèle à (AB) passant par N coupe (BC) en R.
Le cercle circonscrit au triangle MNR recoupe les côtés du triangle
ABC en P, Q et S.
Nous obtenons une configuration de six points, situés sur un cercle de Tücker.
Propriétés
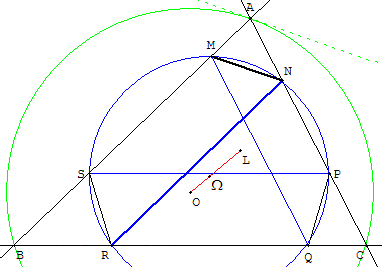
Les droites parallèles (AB) et (NR) coupent le cercle
suivant deux cordes égales, d'où MN = SR.
(RS) antiparallèle à (AC) par rapport à (BA, BC) :
(RS, BA) = (RS, RN) car (BA)//(RN)
(RS, RN) = (MS, MN) = (AB, MN), angles inscrits de droites
(AB, MN) = (BC, AC) car les droites (MN), (BC)
sont antiparallèles aux droites (AB), (AC).
On a donc (RS, BA) = (BC, AC) : les droites (RS), (AC)
sont antiparallèles aux droites (BA), (BC).
(MQ) parallèle à (AC) :
(MQ, AC) = (MQ, MN) + (MN, AC)
(MQ, MN) = (RQ, RN) = (RQ, AB), angles inscrits de droites
(MN, AC) = (AB, BC) car les droites (MN), (BC)
sont antiparallèles aux droites (AB), (AC)
(MQ, AC) = (RQ, AB) + (AB, BC) = (RQ, BC) = 0.
(MQ) // (AC). Ces parallèles coupent le cercle suivant
deux cordes égales, d'où MN = PQ et MN = PQ = SR.
De l'égalité PQ = SR il résulte le parallélisme de (BC) et (SP).
Un calcul d'angles analogue au premier calcul permet de déduire
que (PQ) est antiparallèle à (AC) par rapport à (BA, BC).
Conclusions
Les six points jouent des rôles analogues.
Par chaque point on mène deux droites :
l'une parallèle à la tangente à (Γ) en l'un des sommets du côté qui le porte,
et l'autre parallèle à l'autre côté issu de ce sommet.
Par tout point d'un côté distinct des sommets passe deux
cercles de Tückerobtenus en considérant les deux
tangentes à (Γ) aux deux sommets des côtés qui le porte.
Triangle tangentiel à UVW
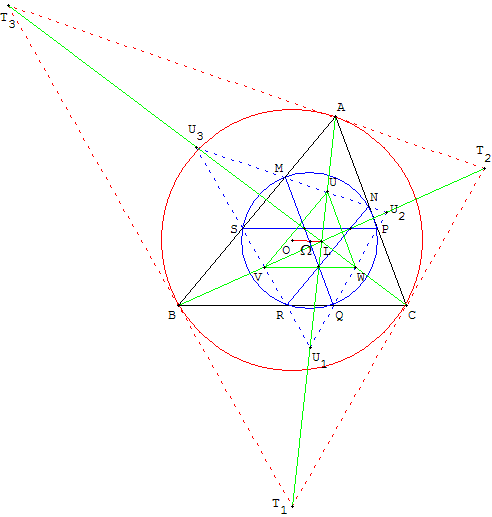
Les points U1, U2 et U3, intersections des droites (PQ), (RS) et (MN), s
ont situés sur les symédianes. Le triangle U1U2U3 est le triangle tangentiel
de UVW, il est homothétique du triangle tangentiel T1T2T3 de ABC,
dans une homothétie de centre L.
Voir : Symédianes
Autre construction du cercle à partir de M et N
À partir d'un point M de (AB) distinct de A, mener la
parallèle à la tangente en A à (Γ). Elle coupe (AC) en N.
Construire les points U2 et U3, intersection de (MN) avec les
symédianes (CL) et (BL). Tracer les droites (RS) et (PQ) parallèles
aux tangentes à (Γ) en B et C et trouver les quatre autres points du cercle.
Construction de trois antiparallèles de longueur égale
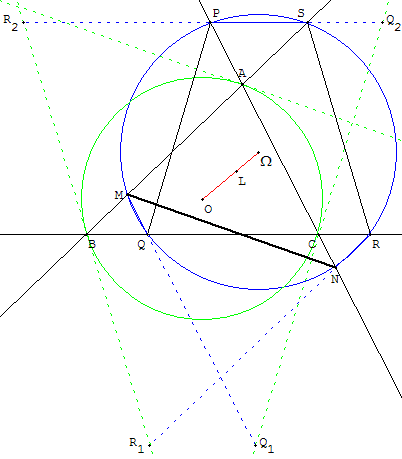
Définition 3 : Les droites (MN), (PQ) et (RS) sont antiparallèles
aux côtés
du triangle et les segments qu'elles déterminent
sont de même longueur.
Cette propriété peut être prise comme définition en déterminant
trois segments [MN], [PQ], [RS] de longueur égale et parallèles
aux tangentes en A, B, C au cercle circonscrit.
Construction
À partir d'un point M de (AB) distinct de A, mener la parallèle
à la tangente en A à (Γ), donc perpendiculaire à (AO).
Elle coupe (AC) en N. Reporter la longueur MN sur la tangente
en B à (Γ) en R1 et R2, sur la tangente en C en Q1 et Q2.
La parallèle à (AB) passant par R1 coupe (BC) en R,
la parallèle à (BC) passant par R2 coupe (AB) en S.
La parallèle à (AC) passant par Q1 coupe (BC) en Q
et la parallèle à (BC) passant par Q2 coupe (AC) en P.
Nous obtenons une configuration de six points,
ces points sont cocycliques et situés sur un cercle de Tücker.
Justification
La parallèle à (AB) passant par N coupe la tangente en B à (Γ) en R1
et (BC) en R. Par parallélisme, le cercle circonscrit au triangle
MNR recoupe les côtés du triangle ABC en P, Q et S.
Comme on l'a vu dans la définition 2, c'est un cercle de Tücker.
[MN] étant construit, il peut être délicat de choisir,
à partir de B, la direction vers R1 ou R2 pour placer R.
Ce n'est pas un problème pour le logiciel.
Milieux des cordes, construction à partir d'un centre donné
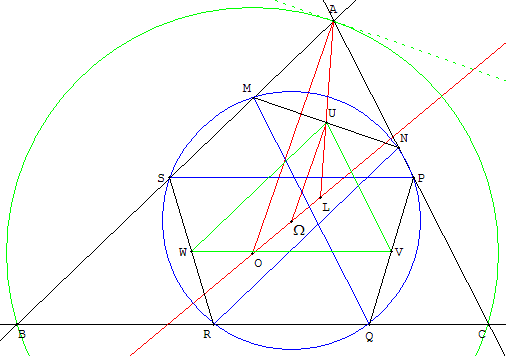
Les milieux forment un triangle UVW se déduisant de ABC
dans une homothétie de centre L de rapport t avec |t| = LU/LA.
Dans cette homothétie, le point O a pour image Ω avec LΩ/LO = |t|.
Ce point Ω est le centre du cercle circonscrit à UVW.
La droite (UΩ) parallèle à (OA) est perpendiculaire à (MN),
c'est la médiatrice de [MN].
De même, la droite (VΩ) est la médiatrice de [PQ].
Le point Ω est bien le centre du cercle de Tücker (T).
Un cercle de Tücker est caractérisé par son
centre Ω situé sur (OL), distinct de O et de L.
Construction
La parallèle à (OA) passant par Ω coupe (LA) en U.
M et N sont situés sur la perpendiculaire en U à (OA) et on complète R
par parallélisme pour tracer le cercle circonscrit à MNR.
Deux cercles de Tücker
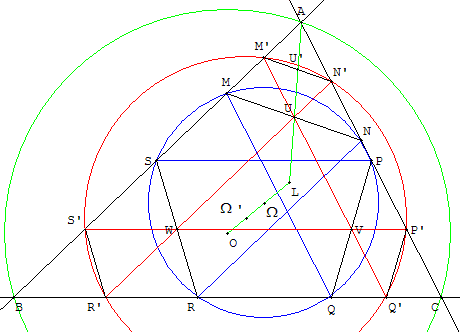
|t| = LU/LA.
En prolongeant les côtés du triangle U’V’W’ jusqu'à ceux du triangle ABC,
nous obtenons un deuxième cercle de Tücker passant par M’N’P’Q’R’S’.
En prenant les milieux des cordes [M’N’], [P’Q’], [R’S’],
le triangle U’V’W’ est homothétique du triangle ABC
dans une homothétie de centre L de rapport t’ :
|t’| = LU’/LA = |(t+1)/2| (en effet, le point U’ est le milieu de [UA]).
Autres propriétés de la figure
PR = QS, MP = NQ, NS = MR.
Les triangles NQS et MPR sont directement semblables à ABC.
WikiPédia : cercles de Tücker
5. Cercles de Lemoine
Deux cas particuliers de cercles de Tücker :
Premier cercle de Lemoine
Lemoine Émile, 1840-1912
Tücker Robert 1832-1905
Les parallèles aux côtés d'un triangle menées par le point
de Lemoine coupent les côtés en six points, cocycliques.
Le centre O’ est le milieu de [OL] où O est le centre du cercle circonscrit.
Les droites (RQ), (ST) et (PU) sont antiparallèles aux côtés d'un triangle.
Les segments sont de même longueur et leurs milieux A’, B’ et C’
situés sur les symédianes forment un triangle A’B’C’ homothétique
du triangle ABC dans une homothétie de centre L.
L'hexagone PQRSTU est dit hexagone de Lemoine.
Deuxième cercle de Lemoine
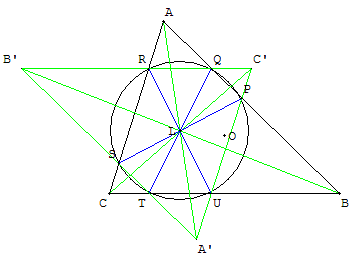
Les antiparallèles aux côtés d'un triangle ABC,
menées par le point de Lemoine L, coupent
les côtés du triangle en six points cocycliques.
Ces points sont situés sur le deuxième cercle de Lemoine centré en L.
Les points d'intersection A’, B’, C’ des droites
(RQ), (ST) et (PU) sont situés sur les symédianes.
Ils forment un triangle A’B’C’ symétrique du triangle
ABC dans une symétrie de centre L.
Autre cercle de Tücker : cercle de Taylor
WikiPédia : cercles de Lemoine
Cercles remarquables
Autres cercles remarquables du triangle
Cercle pédal
Cercle podaire
Cercle de Thalès du triangle rectangle :
le demi-cercle dont le diamètre est l'hypoténuse.
Trois cercles égaux tangents dans un triangle
GeoGebraBook : Géométrie du triangle
Recherche de triangles connaissant :
– trois droites remarquables,
Sur ordinateur, cette page en grand écran
La première page de ce document n'est pas une image
et une copie ne devrait pas être référencée par Google
qui onsidère l'URL de ce document comme une erreur de type "soft 404".
Copyright 2002 - © Patrice Debart
|
|
Page no 97, créée le 17/11/2002 |