Descartes et les Mathématiques

Le nombre d'or

Nombre d'or, section d'or, rectangle d'or,
triangle d'or, spirale d'or, suites de Fibonacci,
puissances de φ, suites de pentagones.

Sommaire

1. Le nombre d'or

2. Éléments d'Euclide

3. Constructions classiques
        Construction de φ
        Section d'or

        Construction d'Euclide

4. Nombre d'or et trigonométrie

5. Rectangle d'or

        Tracé régulateur

        Pavage

        Spirale logarithmique

6. Triangle d'or

        Pavage

        Spirale d'or

7. Suites et nombre d'or

8. Suites de Fibonacci - puissances de φ
        Suites de pentagones

Le nombre d'or n'est presque nulle part. Certains le voient partout !

L'harmonie a le plus souvent affaire avec le 5/3
de nos écrans qu'avec le nombre d'or.

Les proportions du Parthénon résistent fortement
à l'idée à quantifier le beau et le nombre d'or,
qui sera explicité 200 ans plus tard, devait être
très loin des préoccupations de Phidias.

1. Nombre d'or (ou section dorée ou encore divine proportion)

en : golden ratio in geometry

Partage d'un segment, appelé par Euclide, en « moyenne raison » :

Trois points A, B et M alignés forment une section dorée
si le point M du segment [AB] est tel que : = ,
ce qui signifie que le grand et le moyen segment sont
dans le même rapport que le moyen et le petit segment (AB > AM > MB).

Le rapport est, comme le montre les calculs ci-dessous,
égal au nombre d'or φ = ≈ 1,618 034 :
on a le partage d'un segment qu'Euclide réalise sans calcul.
Au 15^e siècle, avec le régne de la religion, le moine franciscain
Luca Pacioli le nomme proportion divine, il devient d'or
avec la montée du capitalisme au 19^e.
Ceci est bien loin des préoccupations des mathématiciens
pour qui c'est un nombre irrationnel constructible comme un autre.

Calculs algébriques

Soit un segment [AB] de longueur 1 et un point M
de [AB] tel que AM = x, d'où MB = AB − AM = 1 − x.

Le point M partage [AB] suivant la section d'or si on
a l'égalité des rapports  et :
de = et = , on en tire = .

Le produit des « extrêmes » 1 − x est égal au produit
des « moyens » x² : x² = 1 − x, d'où l'équation x² + x − 1 = 0.

Cette équation a pour solution positive x = = = φ − 1,
où φ =  est le nombre d'or.

Le rapport = , inverse de , est donc égal au nombre d'or φ :
le point M réalise une section dorée du segment [AB].

2. Éléments d'Euclide - Le triangle d'or dans le livre IV

La découverte du nombre d'or remonte à l'antiquité grecque.
On a cru un temps que des figures de l'Égypte antique se
rattachaient au nombre d'or, mais c'était pur hasard et superstition.

Pour les « anciens Grecs », le nombre d'or apparaît comme
un nombre irrationnel, lié aux problèmes du partage d'un
segment en « moyenne et extrême raison »
et aux propriétés des pentagones et décagones.

L'essentiel des propriétés du nombre d'or se trouve dans
les Éléments d'Euclide, qui ne lui donne pas de nom particulier,
et qui était détaché de toutes les préoccupations mystiques
qui entoureront ce nombre à partir du XV^e siècle.

Les éléments d'Euclide - livre IV - Proposition 10

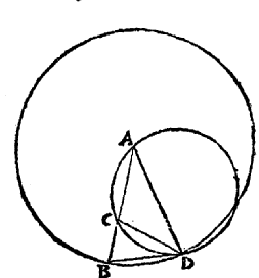
Dans ce problème, Euclide
définit l'inverse du nombre
d'or comme la longueur
AC, où le point C sur un
segment AB (que nous
considérons comme
unitaire) de telle façon que :

AC² = AB × BC.

Pour nous x² = 1 × (1 − x).
Cette équation x² + x − 1 = 0
a bien pour solution positive

x = .

Le point C partage le segment [AB] en moyenne raison.

Sur le cercle de cercle A, passant par B,
Euclide place le point D tel que BD =AC.

ABD est un triangle d'or.
Les angles à la base (72°) sont doubles de l'angle au sommet (36°).

Voir la construction d'Euclide du pentagone avec ce triangle d'or

3. Triangle rectangle où un des
petits côtés est la moitié de l'autre

3.a. Construction de φ

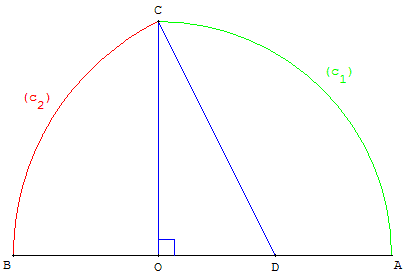
Tracer un angle droit de sommet O. Un cercle (c₁)
de centre O, coupe les côtés de cet angle en A et C.
On choisira comme unité le rayon OA.

D est le milieu de [OA],
le cercle de centre D et de rayon DC coupe (OA) en B.

La longueur du segment [AB] est φ.

Remarque : le point O réalise une section dorée du segment [AB] :
OB = .

Indications

En effet, d'après la propriété de Pythagore
dans le triangle rectangle OCD, on a :

CD² = CO² + OD² = 1² + ()² = d'où CD = .

AB = AD + DB = + = = φ.

Remarque

Le triangle rectangle de côtés proportionnels à 1,
et est utilisé depuis l'antiquité pour le tracé
de sections dorées.

On le trouve, accolé à un triangle rectangle isocèle, dans
de nombreuses constructions à la « règle et au compas »  :

rectangle d'or

« rectangle »

triangle d'or

pentagone régulier

décagone

3.b. Section d'or

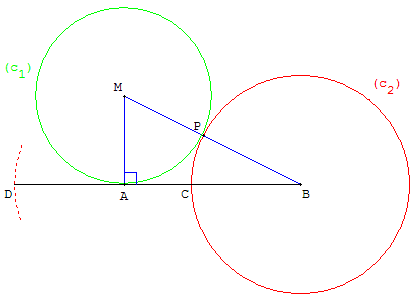
Partage d'un segment en « extrême et moyenne raison »

À partir du segment [AB], sur la perpendiculaire en A à (AB),
placer un point M tel que : AM = AB.

Le cercle (c₁) de centre M, passant par A, coupe le segment [MB] en P.

Le cercle (c₂) de centre B, passant par P, coupe le segment [AB] en C.

Le point C réalise une section dorée du segment [AB] :
= φ.

Soit D le point de la droite (AB), à l'extérieur de [AB] tel que AD = BC.

C et D partagent le segment [AB] en « moyenne et extrême raison »:
= = φ.

Si on choisit AB comme unité, alors DB = φ et CB = .

Indications

En effet, d'après la propriété de Pythagore dans le triangle rectangle AMB, on a :

MB² = AM² + AB² = AM² + (2AM)² = 5 AM² d'où MB = AM.

= 2AM/PB = 2AM/(MB−MP) = 2AM/(MB−AM) =
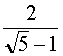= = = φ.

3.c. Construction de la section dorée

Constructions d'Euclide dans le livre VI

Partage d'un segment [AB] en « moyenne et extrême raison :
étant donné deux points A et B, trouver un point D
tel que B, D et A forment une section dorée ; et trouver
un point M tel que A, B et M forment une section dorée.

On considère une droite (AB) et sur la perpendiculaire
à (AB) en A un point C tel que AC = AB.

On note I le milieu de [AB]. Le cercle (c₂) de centre I
et de rayon IC coupe (AB) en D du côté de A.
Le cercle (c₃) de centre A et de rayon AD coupe [AB] en M.

D'après le livre VI des éléments

Preuve par le calcul

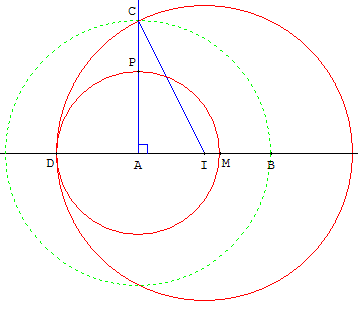
On vérifiera facilement, en prenant AB comme unité (AB = 1) que :
AI = ; CA = AB = 1 ; DI = IC = ;
AM = DA = DI − AI = − = =
= φ − 1 ≈ 0,618 ;
MB = AB − AM = 1 − = 2 − φ ≈ 0,382 ;
DB = DI + IB = + = φ ≈ 1,618.

MA = ; = φ ;
= MB × = (1 − ) × φ = φ − 1 = = .
= d'où = φ : le point M réalise la section dorée du segment [AB].

Remarque : le cercle (c₃) coupe le segment [AC]
en P qui réalise la section dorée de ce segment.

Construction avec deux carrés

Partage d'un segment [AC] en « moyenne raison » :
étant donnés deux points A et C trouver un point P
tel que A, C et P forment une section dorée.

Construction

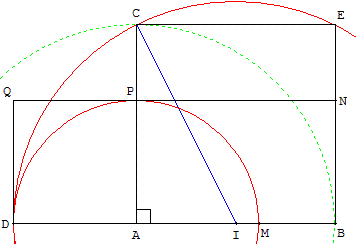
On complète avec le point E le carré de côtés [AB] et [AC],
et avec le point Q le carré de côtés [AD] et [AP].

La droite (QP) coupe (BE) en N.

Preuve par le calcul

Le rectangle PNEC a pour longueur CE = 1
et pour largeur CP = MB = 2 − φ.

Son aire est 2 − φ.

Le carré DAPQ a pour côté AP = AM = .
Son aire est .

Nous avons montré au chapitre 7 que = 2 − φ.
Le rectangle PNEC et le carré CFGH ont la même aire :
CE × PC = AC × PC = AP².

= : on a bien une section dorée du segment [AC].

Autre construction

3.d. Corde et tangente égales

Construction du forum futura-sciences :

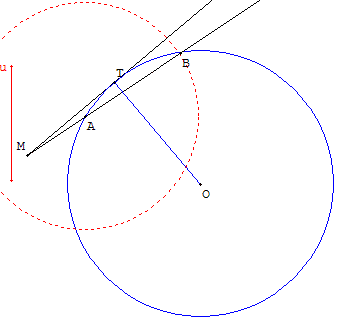
Soit deux points M et T du plan tels que MT = 1
Un cercle (c) est tangent en T à la droite (MT).
{Le centre O du cercle est situé sur la perpendiculaire en T à (MT)}

Étant donné un point A du cercle (c), sur la demi-droite [MA), à l'extérieur
du segment [MA] placer le point B tel que AB = 1 et tel que B soit sur (c).

Déplacer le point A de telle façon que B, intersection de [MA)
et du cercle de centre A, de rayon 1, soit situé sur le cercle (c).

1. Montrer que MA × MB = MT².
2. Montrer que le rapport est égal au nombre d'or.

Indications

1. La puissance de M par rapport au cercle (c) est MA × MB
et est égale au carré de la tangente MT.

2. AB = MT = 1. Posons MA = x, alors MB = MA + AB = x + 1;
la puissance de M qui est MA × MB = MT², s'écrit x(x + 1) = 1²,
d'où l'équation x² + x − 1 = 0 qui, comme nous l'avons vu au §1,
a pour solution positive x = = ;
MB = x + 1 = + 1 = φ.

Les trois points M, A, et B forment une section dorée.
Le rapport est égal au nombre d'or φ.

4. Nombre d'or et trigonométrie

On a vu dans la page angle trigonométrie que cos est égal à
la moitié du nombre d'or φ = 2 cos = ;
cos = − cos = .

En appliquant la formule de duplication cos 2a = 2 cos²a − 1, on trouve :

cos = − cos = sin = 2 cos² − 1 = = = .

x
cos x				−

L'inverse du nombre d'or est donc = φ − 1 = = 2 sin .

5. Rectangle d'or

Dans un rectangle d'or, le rapport de la longueur
sur la largeur est égal au nombre d'or φ = .

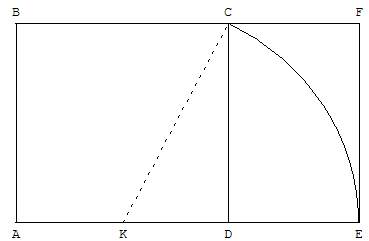
Depuis l'antiquité grecque, on sait construire un
rectangle d'or d'une largeur donnée de la façon suivante :
  • tracer un carré ABCD ayant comme côté la largeur souhaitée,
  • prendre le milieu K de [AD],
  • rabattre le point C sur (AD) en traçant le cercle de centre K,
        passant par C. Ce cercle coupe [AD) en E,
  • terminer la construction du rectangle d'or ABFE.

En effet, en choisissant la largeur AB comme unité, on a KE = KC = ,
d'après la propriété de Pythagore dans le triangle DKC rectangle en D,
et AE = + = φ.

5.b. Diagonales des rectangles d'or

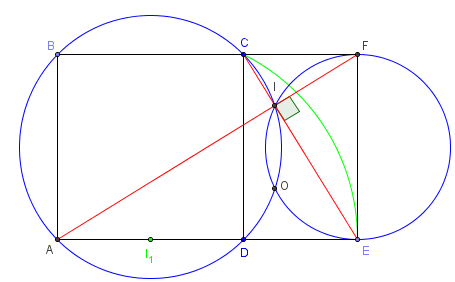
À partir d'un carré ABCD, la diagonale [AF] du grand
rectangle d'or ABFE est perpendiculaire à la diagonale
[CE] du petit rectangle d'or CFED.

Cette propriété se retrouve en terminale S, avec
la similitude de centre O et d'angle – 90°
qui transforme A en C, et F en E.
Cette similitude transforme les rectangles d'or :
ABFE en CFED.

La diagonale [AF] a pour image [CE] et elles sont bien
perpendiculaires : leur angle est égal à la valeur absolue
de l'angle de la similitude.

Le centre O et le point I, intersection de ces deux diagonales,
sont les deux points d'intersection des cercles de diamètres [AC] et [FE].

Figure interactive dans GeoGebraTube :
       diagonales des rectangles d'or

Perpendiculaires et rectangles d'or

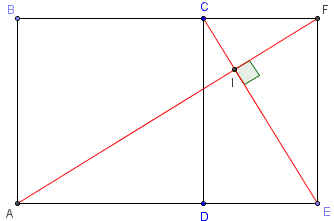
Grâce à cette propriété est caractéristique, à partir du carré
ABCD, en déplaçant le point E sur [AD) de telle façon que
les diagonales [AF] et [CE] soient perpendiculaires,
on peut trouver un rectangle d'or qui donne le nombre d'or φ.

Avec un logiciel de géométrie dynamique, il est en
principe possible de retrouver cette configuration
(j'ai un peu triché pour éditer la figure !)

Les anciens Égyptiens auraient utilisé cette propriété.
On peut se poser la question de savoir comment on
peut ainsi inverser cause et conséquence sans
connaître le nombre d'or ?
Des recherches minutieuses dans les pyramides n'ont
pas permis de retrouver le CD de GeoGebra utilisé !

Figure interactive dans GeoGebraTube :
        construction de rectangles d'or

Commande GeoGebra : déplacer le point E

5.c. Tracé régulateur

En architecture, comme en dessin, le tracé régulateur
permet de schématiser les lignes de force d'une figure.

« Le tracé régulateur n'apporte pas d'idées poétique ou lyrique ;

il n'inspire nullement le thème ; il n'est pas créateur ; il est équilibreur. »

Le Modulor - Le Corbusier - 1948

5.c.2. Tracé régulateur dans un rectangle d'or

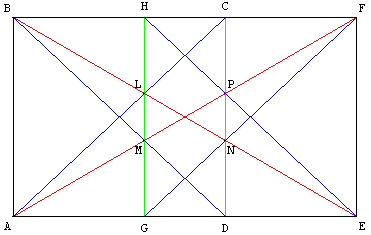
Les diagonales du rectangle rencontrent les diagonales
des carrés selon des sections d'or.

Les diagonales des carrés ABCD et EFHG coupent en L, M, N, P
les diagonales du rectangle d'or ABFE.

Section d'or sur une diagonale : AF/AP = AP/AM = φ.

Section d'or sur un côté des carrés : CD/CN = CN/CP = φ.

5.c.3. Tracé régulateur dans un « rectangle »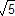

« Rectangle » :

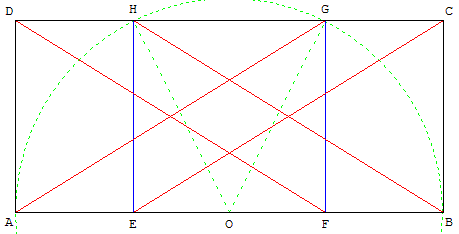
Le rapport entre la longueur et la largeur est .
Le rectangle est la juxtaposition d'un carré de côté 1
et deux rectangles d'or de longueur 1 et de largeur .

AFGD et EBCH sont des rectangles d'or de longueur φ et de largeur 1.

Construction à partir d'un carré de côté [EF] tel que EF = 1.
Soit O le milieu de [EF].
Le cercle de centre O, passant par H, coupe (EF) en A et B.
Compléter le rectangle avec C et D sur (GH).

ABCD est un « rectangle » de longueur 1 et de largeur .

Voir : inscrire un carré dans un demi-cercle

5.c.4. La Présentation de la Vierge au Temple

Titien 1488-1576, Académie de Venise

L'escalier est parallèle à une des diagonales du rectangle d'or de droite.

Plus contestable : il comporte 8 et 5 marches, une suite de Fibonacci.

Le centre est dans la lumière, deux rectangles d'or de chaque côté
sont dans l'ombre.

La petite fille, à l'intersection des diagonales du rectangle d'or
de droite, est la vierge ;
la femme à la coiffe drapée blanche c'est sa mère, sainte Anne.

Tout cela c'est bien beau, mais les dimensions du tableau ne
respectent pas la divine proportion et le tracé régulateur
n'a rien à voir avec le rectangle d'or !

Figure interactive dans GeoGebraTube :
      tracé régulateur - Présentation de la Vierge

5.c.5. Carré inscrit dans un demi-cercle

L'École d'Athènes
− Raphaël, vers 1510 −
Musée du Vatican

Le côté du carré jaune est égal au diamètre du cercle, divisé par .
Cette construction classique est habituellement réalisée en 1^ère S
avec les homothéties, mais peut être résolue par le calcul
en classe de seconde.

5.d. Pavage du plan avec des rectangles d'or

Pavage non périodique de rectangles d'or

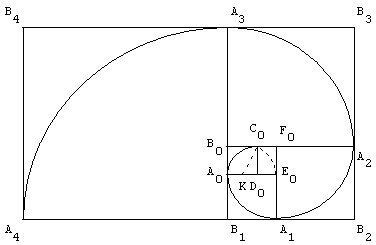
Il est possible de paver le plan à partir de rectangles d'or.
Ce pavage non régulier est formé de rectangles de plus en plus grands.

Ces rectangles sont obtenus en ajoutant au rectangle un carré
qui est le gnomon de ce rectangle, gnomon qui permet d'obtenir
un nouveau rectangle semblable au précédent.

Joconde et spirale d'or

Le nombre d’or a fasciné mais
il n'existe pas de loi
mathématique de l’esthétisme.

Dans les années 30,
avec Matila Ghyka,
les adeptes du
nombre d’or ont disséqué
les œuvres d’art pour
y déceler ce nombre.

Par exemple sur la Joconde
ci-contre, on trouve une
approximation du
nombre d’or, mais
le rectangle d'or contenant la spirale
est bien éloigné du format du tableau !

5.d.2. Spirale logarithmique

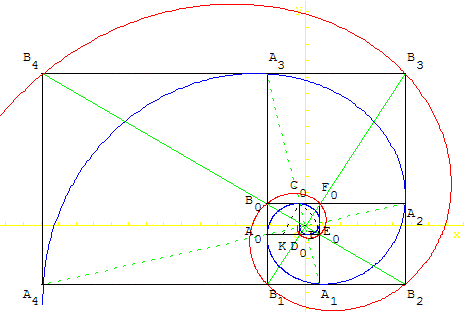
La spirale dorée est approchée par une spirale
logarithmique d'équation en coordonnées polaires
ρ = aφ^(2q/p) dans un repère d'origine I point
d'intersection de diagonales des rectangles d'or (voir figure).

C'est la spirale miraculeuse (spira mirabilis) de Jacob Bernouilli.

Une autre spirale logarithmique passe par les sommets des rectangles d'or.

6.a. Nombre d'or dans le triangle égyptien

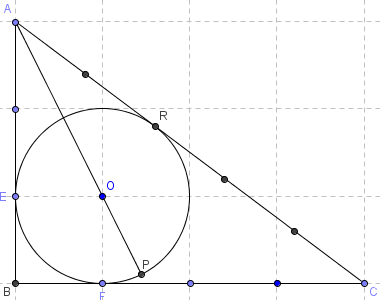
Dans le triangle rectangle égyptien 3 ; 4 ; 5, on trace le cercle
inscrit de centre O, de rayon 1, tangent en E, F et R aux côtés du triangle.

Dans le triangle rectangle AEO de petits côtés 2 et 1, l'hypoténuse mesure .
La bissectrice (AO) coupe le cercle inscrit en P,
tel que AP = + 1.

En divisant AP par 2, on trouve le nombre d'or φ = .

Les anciens Égyptiens ne savaient pas le théorème
de Pythagore, ni le calcul sur les racines.
Il semble difficile qu'il puissent utiliser une telle
figure pour trouver le partage en moyenne raison  ?

Figure interactive dans GeoGebraTube : triangle égyptien

6.b. Triangle d'or, triangle d'argent

Le triangle d'or (ou triangle sublime, ou triangle d'Euclide)
ACD est un triangle isocèle en C d'angle , les deux autres
angles à la base en A et D étant égaux à .

Le rapport entre le grand côté et la base est égal au nombre d'or :

= = φ.

Soit B le point qui partage [AC] en une section d'or :
Q = = φ, on a DA = DB = BC, (DB) est la bissectrice de l'angle ADC.
Le triangle isocèle ABD est semblable au triangle ADC avec
un rapport de similitude égal à φ. Ce triangle ABD est aussi un triangle d'or.

Le triangle BCD est un triangle d'argent, isocèle en B d'angle ,
les deux autres angles, en C et D, étant égaux à .
Le rapport des côtés est aussi égal au nombre d'or : = φ.

6.c. Pentagone régulier

Un triangle d'or et deux triangles d'argent

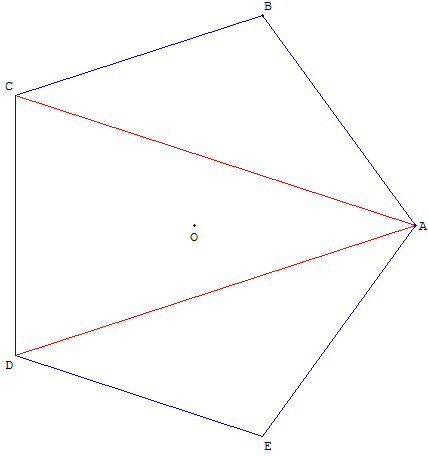
Un pentagone régulier est formé par un
triangle d'or et deux triangles d'argent.

Dans le pentagone ABCDE, ACD est un
triangle d'or, ABC et ADE sont des triangles d'argent

C'est harmonique, Euclide n'y voyait que de l'or.
L'obscurantisme de la « géométrie sacrée »,
aidé par les druides d'Internet, confère au pentagone un caractère divin.

Pentagone régulier et nombre d'or

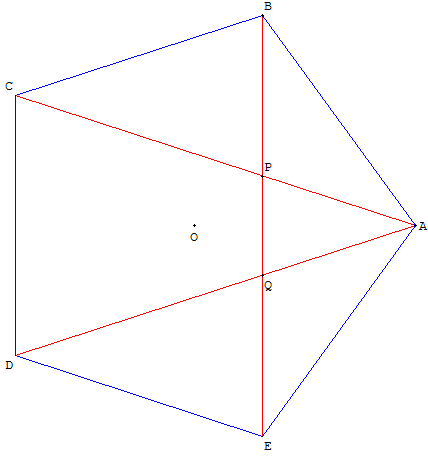
PE = BQ = BA.

Le rapport est égal au nombre d'or : BA/BE = φ.

Le point P divise [BQ] et [BE] dans le rapport du nombre d’or :

BP/BQ = PE/BE = φ.

Les points P et E divise [BQ] en « moyenne et extrême raison ».

Triangle bisocèle : voir triangle au collège

6.d. Construction du triangle d'or à partir du grand côté

Si A et C sont deux sommets du triangle, soit B
le point qui partage [AC] en une section d'or.
Le troisième sommet D est un des points d'intersection du
cercle c₃ de centre C, passant par A et du cercle c₄ de centre B, passant par C.

Soit α = l'angle au sommet du triangle d'or. α est aussi
égal à l'angle du triangle d'or isométrique. = 2α
car (DB) en est la bissectrice.
La somme des trois angles du triangle d'or est
+ + = α + 2α + 2α = 5α = π.

α = . Le triangle d'or a donc un angle au sommet de ,
les deux autres angles étant égaux à .

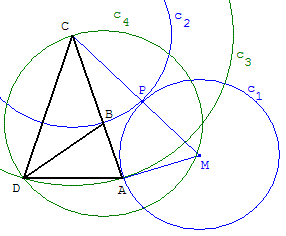
6.e. Construction du triangle d'or à partir de la base

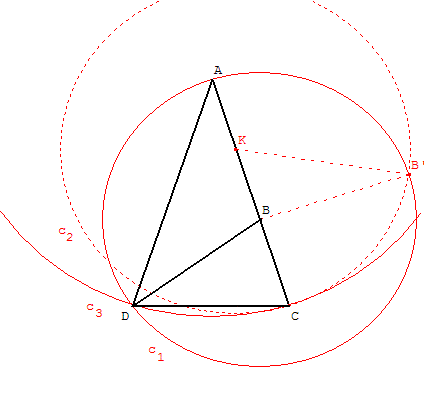
À partir du segment [AB] trouver un point C et tracer un
triangle d'or ayant une base [DC] égale à AB.

On adapte ici le procédé de construction du rectangle d'or

Soit K le milieu de [AB] et B’ le point de la droite perpendiculaire
en B situé sur le cercle c₁ de centre B passant par A, tel que le
triangle ABB’ soit rectangle isocèle direct (cf. figure).

Le cercle c₂ de centre K passant par B’ coupe la demi-droite [AB) en C.

B est la section dorée de [AC].

En effet, si la longueur AB représente l'unité, la propriété de Pythagore
dans le triangle
rectangle KBB’ permet de vérifier que :

AC = AK + KC = AK + KB’ = + = φ.

Une des intersections du cercle c₃ de centre A passant par C
avec le premier cercle c₁ de centre B est D.
ACD est un triangle d'or.

6.f. Pavage non périodique du plan avec des triangles d'or

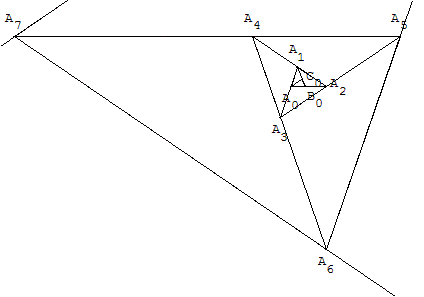
Il est possible de paver le plan à partir de triangles d'or.
Ce pavage non régulier est formé de triangles de plus en plus grands.

À partir du triangle A_nA_n+1A_n+2 créer le point A_n+3 tel
que A_n+1A_nA_n+3 soit une section d'or et recommencer.

Ces triangles sont obtenus en ajoutant au triangle un
triangle d'or qui est le gnomon de ce triangle, gnomon qui
permet d'obtenir un nouveau triangle semblable au précédent.

6.g. Spirale d'or

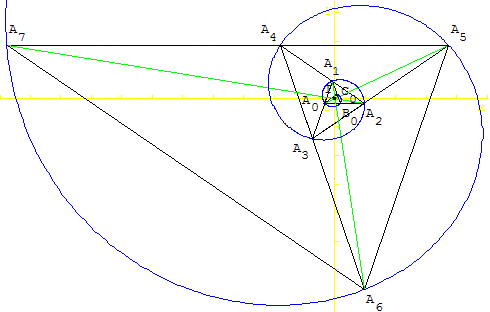
Une spirale logarithmique d'équation, en coordonnées polaires,
ρ = aφ^(5q/3p) dans un repère d'origine I, intersection des droites
A₀A₅ et A₁A₆ (voir figure), passe par les sommets des triangles d'or.

7. Suites et nombre d'or

Étudier la suite numérique u_n définie par u₀ = 0 et
pour tout n positif par : .

La limite l de cette suite est le nombre d'or φ = .
C'est la solution de l'équation irrationnelle ;
solution positive de l'équation du second degré :

x² = x + 1, soit x² − x − 1 =  0.

Le produit des solutions de cette équation est −1,
la solution négative est l'opposé de l'inverse du
nombre d'or : β = − . En divisant l'équation par x, non nul, on obtient :
x − 1 − = 0 soit x = 1 + ,
d'où φ = 1 + . φ et ont donc la même partie décimale 0,618 033 988 75…
On retrouve donc la définition de Luca Pacioli,
donnée dans son ouvrage la divine proportion en 1509 :
« Le nombre d'or est tel que si on lui ajoute l'unité
et qu'on le divise par lui-même on le retrouve »

On pourra montrer que la suite v_n, définie par v₀ = 0
et pour tout n positif par : , a pour limite φ.

Remarque : au XIX^e siècle on utilise la lettre grecque
φ (phi) pour le nombre d'or, en hommage au sculpteur grec Phidias.
Platon affirmait que toute la connaissance réside en ce nombre.

C'est suffisant pour inventer le mythe du Parthénon :
la façade serait inscrite dans un rectangle d'or.
Même en rajoutant le fronton « triangulaire », Phidias est loin de l'or !

7.b. Mythe de la pyramide de Khéops

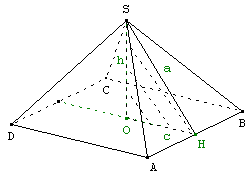
À la fin de sa construction,
la hauteur h de la pyramide
de Khéops était OS = 146 m.

Le côté AB  =  2 c mesure 232 m.
À 1 % près, la hauteur de la
pyramide est égale à la moitié
du côté multiplié par .

On a = = d'où = φ.
Les trois côtés du triangle SOH forment
une suite géométrique de raison .
SOH est aussi improprement dit triangle égyptien.

Voir : cos et pentagone

La moitié du côté de la base multipliée par le nombre d'or
est égale à la hauteur des faces latérales de la pyramide

La demi-face SHA de la pyramide est la moitié d'un
rectangle d'or de longueur SH = a et de la largeur AH = c.

Les faces latérales sont donc formées de deux demi-rectangles d'or.
Cela correspond à une valeur approchée de pour π.
Mais cette valeur 3,144 est bien loin du de la valeur ≈ 3,16
qu'ils utilisaient pour π (papyrus de Rhind).

Cette coïncidence est d'autant plus impossible que les
« anciens Égyptiens » ne connaissaient pas le nombre d'or et que
les outils mathématiques nécessaires pour le calculer
n'apparaîtront à Babylone que 7 siècles plus tard.

Après l'échec de la quadrature du cercle, entre contre-vérités
historiques et paranoïa, les mystiques des nombres se
défoulent maintenant sur le nombre d'or.

8. Nombre d'or et suites de Fibonacci
Puissances de φ

On a démontré ci-dessus que φ = est la solution positive
de l'équation du second degré x² = x + 1, soit φ² = φ + 1.

On peut facilement démontrer par récurrence que l'on a : φⁿ = a_nφ + a_n−1

avec pour n > 0, a_{n + 1} = a_n + a_n−1 et a₀ = 0 ; a₁ = 1.
a_n est la suite de Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21, 34…

8.b. Suites de pentagones et nombre d'or

Tous les pentagones réguliers sont semblables.

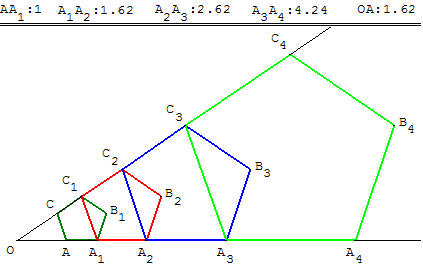
Le pentagone A₁A₂B₂C₂C₁ est l'image du pentagone AA₁B₁C₁C
par l'homothétie de centre O et de rapport φ (nombre d'or).

Les longueurs AA₁, A₁A₂, A₂A₃, A₃A₄ sont égales
aux puissances du nombre φ.

AA₁ = 1, A₁A₂ = φ,
A₂A₃ = φ² = φ + 1,
A₃A₄ = φ³ = 2 φ + 1…

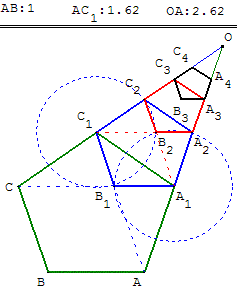
AA₁ = 1, A₁A₂ = φ^{– 1},
A₂A₃ = φ^{– 2}, A₃A₄ = φ^{– 3}…

8.c. Puissances négatives de φ

On a aussi démontré ci-dessus que
φ = 1 + donc = φ − 1 = .

Calculons les puissances négatives
suivantes de φ :

φ^{– 2} = = = = 1 −
        = 1 − (φ − 1) = − φ + 2.

De même, φ^{– 3} = = = = −1 + = −1 + 2(φ − 1) = 2φ −3,
et φ^{– 4} = = = = 2 − = 2 − 3(φ − 1) = − 3φ + 5 et ainsi de suite.

On peut enfin démontrer par récurrence que l'on a : φ^{− n} = b_n−1φ + b_n,
avec pour n > 0, b_n+1 = − b_n + b_n−1 et b₀ = 1 ; b₁ = − 1 ;

b_n = (−1)ⁿa_n+1 est la suite de Fibonacci alternée :
    1, −1, 2, −3, 5, −8, 13, −21, 34…

Voir : récurrence double - Fibonacci

Table des matières

Google friendly ; sur ordinateur, cette page en grand écran

Dans d'autres pages du site

Histoire des mathématiques

Pentagone régulier :
    constructions exactes
    constructions approchées

Polygone régulier : décagone