Descartes et les Mathématiques
Fonctions en seconde
Figures classiques avec GeoGebra - Capes externe de mathématiques
Un exercice menant à un problème d'optimisation :
deux cadres dans l'écran GeoGebra ; le cadre de gauche pour la figure géométrique,
le cadre de droite pour une fonction permettant la recherche d'extrema.
La statue de la Liberté de New York
Comment varie l'angle sous lequel on voit un objet en fonction de la distance de l'observateur au pied de l'objet ?
Source : Organiser l'enseignement autour d'un PER en classe de Seconde
L'exemple des fonctions
La situation et les données
La statue de la Liberté, érigée en 1886, est haute de 46,50 m sans son socle et de 93 m avec socle.
Arrivant à New York droit sur Liberty Island, un touriste placé à l'avant d'un bateau regarde la
statue. Il a son œil placé à 5 m au-dessus de la mer.
Sous quel angle le touriste voit-il la statue de la Liberté ?
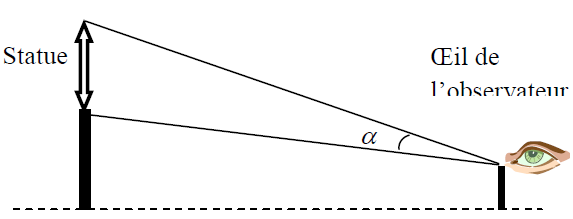
La figure ci-dessus résume la situation :
pour un objet donné, on appelle l'angle de vision, l'angle sous lequel la statue est vue dans sa totalité.
Partie A : À votre avis :
1 - l'angle de vision ne varie pas quand on s'approche de la statue
2 - l'angle de vision diminue quand on s'approche de la statue
3 - l'angle de vision augmente quand on s'approche de la statue
4 - autre proposition
Partie B : La situation est représentée sur une feuille de travail GeoGebra de la manière suivante :
– la statue et son socle sont assimilés à deux segments verticaux portés par la même droite,
– l'observateur est assimilé à un segment vertical, qui représente la hauteur de son œil par rapport au niveau de la mer.
Comment varie l'angle de vision au fur et à mesure que le bateau se rapproche de la statue ?
Géométrie avec GeoGebra
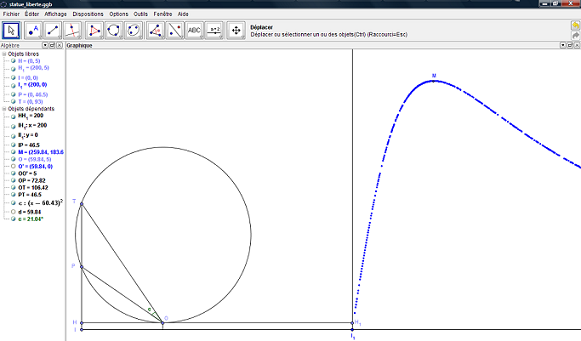
Figure interactive de GeoGebraTube : statue de La Liberté de New York
Avec GeoGebra, déplacer le point O et trouver le maximum pour M !
Soit r le rayon du cercle circonscrit au triangle TPO. L'angle TOP est d'autant plus grand que r est petit. Le cercle de rayon minimum passe par les points T et P et est tangent à (HH1).
Technique GeoGebra
Placer les points dont les coordonnées sont citées dans la fenêtre algèbre. Par exemple, il est efficace de valider dans la ligne saisie H=(0,5)
Placer le point O sur la droite horizontale [HH1] et nommer d le segment[HO].
Pour le graphique, placer un point M et remplacer ses coordonnées par (200 + d, 500α).
Activer la trace de ce point ou bien, en sélectionnant la dernière option du menu droite, tracer le lieu de M piloté par le point O.
Solution
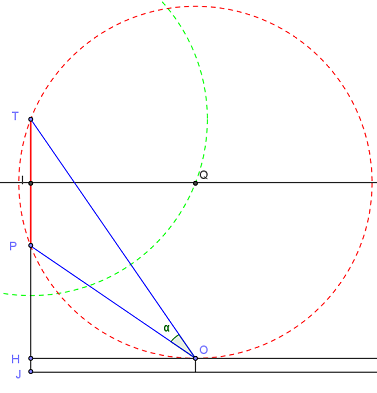
Remarquer que le cercle solution est tangent à la droite horizontale passant par H, son rayon est la longueur IH, où I est le milieu de [TP].
On trouve le centre Q de ce cercle solution comme intersection de la médiatrice de [TP] avec, par exemple, le cercle de centre T et rayon IH.
Lorsqu'on s'approche de la statue, l'angle de vision augmente, jusqu'à ce que l'on se trouve à une distance de 60,43 m.
L'angle de vision maximum est alors α = 21°.
L'angle de vision diminue ensuite quand on s'approche plus près de la statue.
Figure interactive de GeoGebraTube : statue de La Liberté de New York
Voir statue dans géométrie du cercle
La géométrie… avec GeoGebra
La géométrie dynamique au CAPES
Copie Twitter : t.co/GTHc5YX5Li
Mobile friendly
Copyright 2012 - © Patrice Debart
Page no 190, créée le 4/4/2012
mise à jour le 24/11/2013