Descartes et les Mathématiques

La trisection

Sommaire

1. Exercice du Capes 2007

2. Trisection de l'angle de

Analyse

Racine rationnelle d'une équation du troisième degré

Racine constructible d'une équation

3. dicothomie
4. Encadrement par balayage

5. Parties proportionnelles

6. Point fixe - Méthode de Newton

7. Fractions continues

8. Développement de cos(2x)

Dans d'autres pages du site

Utilisation de fonctions en géométrie

La quadratrice de Dinostrate

Conchoïde de Nicomède

Méthode de Chasles

Géométrie synthétique

Méthode de Viète

Méthode d'Archimède

Méthode de Pappus

Pliage d'une feuille

À développer

Trisection de l'angle

Nombre constructible

Par Françoise Bourhis-Lainé

Utilisation de suites pour la recherche de solutions approchées d'une équation numérique
Capes externe de mathématiques 2007 - Épreuve sur dossier

1. Exercice

Le problème de la trisection d'un angle est le suivant : étant donné un angle θ, dont on connaît par exemple le cosinus, on cherche à calculer cos ().
Considérons le cas particulier de l'angle θ = et calculons x₀= cos().
Après avoir fait vérifier que x₀ est « la » solution positive de l'équation 4 x³ − 3x − = 0.
On s'intéressera à la recherche d'une solution approchée à 10⁻² prés.

Travail demandé au candidat

1) Rédiger un énoncé demandant la résolution de l'équation à l'aide d'un algorithme de dicothomie.

2) Rédiger un énoncé correspondant au programme actuel de terminale S, mettant en ouvre une méthode du point fixe.
On pourra remarquer que (E) peut s'écrire sous la forme : x = (3x + )^1/3.

3) Rédiger un énoncé permettant de déterminer x₀ à 10⁻³ près par une méthode de fractions continues, menant au moins à l'encadrement :

x₀ <

4) Montrer que l'équation 8 x³ − 6 x − 1 = 0 n'a pas de racine rationnelle et en déduire que le nombre cos() n'est pas solution d'une équation du second degré à coefficients entiers.

5) Proposer un exercice supplémentaire dans le cadre du thème.

2. Trisection de l'angle

Partager un angle quelconque en trois angles égaux.

Pour la trisection d'un angle θ, il faut trouver t tel que 3t = θ. On a : cos 3t = 4 cos³t − 3 cos t.
Avec la formule cos 3t = 4 cos³t − 3 cos t, en posant cos t = x,
x est une solution de l'équation 4 x³ − 3 x = cos θ.

La trisection revient à savoir si les solutions de cette équation sont constructibles.

D'après Wantzel, pour que la trisection soit possible, l'équation 4 x³ − 3 x − cos θ = 0 doit être réductible au second degré dans Q.

Trisection de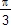

Par exemple, la trisection d'un angle de mesure θ = n'est pas possible :

cos(), solution de l'équation irréductible dans Q[X] : 4 x³ − 3 x − = 0, est algébrique sur Q de degré 3.

Ce qui montre, du même coup, l'impossibilité de construire à la « règle et au compas » l'ennéagone régulier (9 côtés), résultat prouvé en 1801 par Gauss.

Indication

Soit une solution rationnelle irréductible de l'équation 8 x³ − 6 x − 1 = 0. Il s'ensuit, dans Z, l'égalité : 8p³ − 6pq² − q³ = 0.
Il résulte du théorème de Gauss que p divise − 1 et q divise 8. Les candidats pour sont à chercher parmi les facteurs de .

Dans ce cas particulier, de l'égalité : 8p³ − 6pq² = q³, on trouve que q est pair.
Posons q = 2r. Il vient p³ − 3 pr² − r³ = 0.
Mais la fraction étant irréductible p est premier avec q et par suite avec sa moitié r, donc p divise −1 et r divise 1.
Donc p = ±1 et r = ± 1, d'où q = ± 2.
En conséquence x = ± et on vérifie que ± n'est pas solution de l'équation.

Polynôme minimal du troisième degré

P(x) = 8 x³ − 6 x − 1 admet comme solution cos(). Cette solution n'est pas rationnelle.

Soit un autre polynôme Q(x) de Q[X], de degré moindre, qui aurait cos() comme 0.
Si Q(x) était un binôme de degré 1, il admettrait une solution rationnelle ce qui n'est pas le cas.

Q(x) est donc du second degré.
Grâce à la division euclidienne de P(x) par Q(x), on trouve P(x) = Q(x) (ax + b) + R(x), avec a non nul et R(x) binôme du premier degré.

En remplaçant x par cos(), on trouve que R(cos()) = 0, cette solution n'étant pas rationnelle, cette première contradiction impose donc R(x) = 0.
P(x) alors égal à Q(x) (ax + b) serait factorisable dans Q[X] et aurait − b/a pour solution ce qui est impossible.

P(x) est irréductible dans Q[X]. cos() n'est pas solution d'une équation du second degré à coefficients entiers.
cos() est algébrique sur Q de degré 3 et le nombre cos() n'est pas constructible.

Voir aussi une démonstration montrant si l'équation admet une solution constructive, elle admet une solution rationnelle, d'où la contradiction.

Analyse

Racine rationnelle d'une équation du troisième degré à coefficients entiers

Soit P(x) = ax³ + bx² + cx + d un polynôme de degré 3 à coefficients entiers, l'équation P(x) = 0 admet une solution rationnelle x₀ = avec p et q premiers eux, alors p divise d et q divise a.
En effet si est une racine de P(x), on a : ap³ + bp²q + cpq² + dq³ = 0. Il résulte du théorème de Gauss que p divise d et q divise a.

Par exemple pour 8x³ − 6x − 1 = 0. Si une solution existe dans Q, c'est un des facteurs de .
On en déduit que cette équation ne possède pas de racines rationnelles, car les rationnels candidats sont 1, −1, , −, , −, , − ne la vérifient pas.

Si l'équation (E) possède une racine constructible alors elle possède aussi une racine rationnelle

Soit P(x) = x³ + px + q, si P possède une racine constructible alors il possède aussi une racine rationnelle.

Démonstration (à vérifier !)

Le but est de se débarrasser des racines carrées, étape par étape, pour arriver à un nombre rationnel.

Soit a une racine constructible de P, alors il existe une tour d'extension quadratique, suite de corps
Q = K₀ ⊂ K₁⊂ K₂⊂…⊂ K_n ayant les propriétés suivantes :
si i est un entier entre 1 et n alors K_i−1 est inclus dans K_i et K_i est une extension quadratique de K_i−1
et a ∈ K_n et donc a est de la forme a = u + v √µ avec u, v, µ ∈ K_n−1.

P(a) = P(u + v√µ) = r + s√µ = 0 ; r, s, µ ∈ K_n−1 (car dans l'expression de r et s, il n'y a que des u, v, µ, p, q)
si s<>0 => √µ = − r/s
a = u − (vr/s) ∈ K_n−1 on se débarrasse ainsi la racine carrée √µ.
Si s = 0 => r = 0 on prend b = u − v√µ et P(b) = P(u − v√µ) = r − s√µ = 0 ; b est racine de P.
or a + b + c = 0 (avec c troisième racine) c = − 2u ∈ K_n−1
donc soit a est dans K_n−1 ou alors on trouve une autre racine c dans K_n−1 puis on recommence, ainsi on trouve une racine dans K_n−2 puis dans K_n−3… et finalement une racine dans K₀ = Q, c'est-à-dire une racine rationnelle.

Pour la trisection de l'angle, examinons le cas particulier où θ = .

Dans K = Q(cos) = Q() = Q l'équation 4 x³ − 3 x − = 0 devient 8x³ − 6x − 1 = 0.
Le problème est donc de savoir si les solutions de cette équation sont constructibles (tout court, car K = Q) ou non.
Si une solution existe dans Q, c'est un des facteurs de . On en déduit que cette équation ne possède pas de racines rationnelles, car les rationnels candidats sont 1, −1, , −, , −, , − ne la vérifient pas, donc impossible de diviser, à la « règle et au compas », l'angle en 3 parties égales.

3. dicothomie

La fonction f(x) = 4 x³ − 3x − , étudiée sur [0, 1] en raison du cosinus, a pour dérivée f’(x) = 12 x² − 3.
Elle est croissante sur [, 1] ; f() = − et f(1) < 0 sont de signes contraires.
Choisissons a = et b = 1.

D'après le théorème des valeurs intermédiaires, il existe une solution unique x₀ sur l'intervalle [a, b].

La dicothomie est une méthode itérative qui permet d'obtenir de proche en proche des encadrements successifs de plus en plus précis de x₀.
On calcule f pour c = 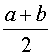, on remplace a par c si f(a) et f(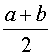) sont de même signe, sinon on remplace b par c.

On arrête l'algorithme lorsque la longueur de l'intervalle est inférieure à la précision p demandée.
Ici p = 10⁻² et le zéro est déterminé au bout de n opérations avec une erreur absolue inférieure ou égale à (b−a)/2ⁿ.

Recherche par dicothomie

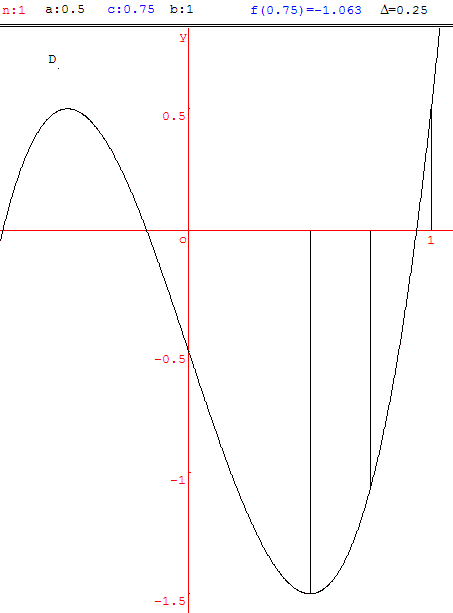
Solution de la dicothomie

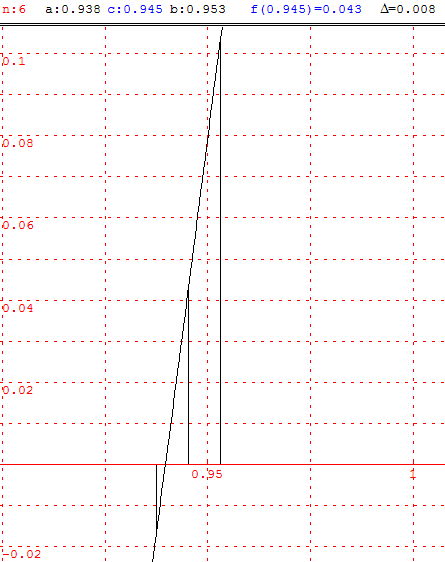
Télécharger la figure GéoPlan trisec_dico.g2w

Solution

Après 6 itérations on a : 0,938 < x₀ < 0,945.

cos() ≈ 0,94 à 10⁻² près.

Algorithme

f(x) = 4*x^3−3*x −
a =
b = 1
Tant que b−a>10⁻² répéter

c= (a+b)/2
Si f(a)*f(c)<0 alors
    b = c
Sinon
    a = c
Finsi
Afficher a, b, f(a), f(b)
Pause

Fin Tant que

Calculatrices TI-92, Voyage 200

rédiger l'algorithme dans l'éditeur de programmes :

dicothomie()
Prgm
4*x^3−3*x−1/2 → f(x)
1/2 → a
1 → b
While b−a>10^(−2)
  (a+b)/2 → c
  If f(a)*f(c)<0 Then
    c → b
  Else
    c → a
  EndIf
    Disp c
  Pause
EndWhile
EndPrgm

Puis exécuter le programme en tapant dans la fenêtre ¨Home :

dichotom()

Excel

Cellule B2 pour a taper 0,5
Cellule D2 pour b taper 1

Cellule C2 taper la formule =(B2+D2)/2 et recopier vers le bas.

Cellule E2 taper la formule de la fonction =4*B2^3−3*B2−1/2 recopier ver la droite en F2 et G2,
sélectionner les trois cellules E2:G2 et recopier vers le bas.

Cellule B3 taper la formule =SI(E2*F2<0;B2;C2) et recopier vers le bas,
cellule D3 taper la formule =SI(F2*G2<0;D2;C2) et recopier vers le bas.

Télécharger la feuille de calcul dicothomie.xls

4. Encadrement par balayage

Avec la calculatrice ou un tableur dresser un tableau de valeur sur [0, 1] avec le pas 0,1 :

Avec Excel taper 0 et 0,1 dans les cases A1 et B1 et recopier ces deux cellules vers la droite jusqu'à la valeur 1,
Cellule A2 taper la formule de la fonction =4*A1^3−3*A1−1/2 recopier ver la droite.

x₀ est dans l'intervalle [0,9 ; 1].

On recommence avec les valeurs 0,9 et 0,91 à recopier vers la droite :

x₀ est dans l'intervalle [0,93 ; 0,94].

On termine avec les valeurs 0,93 et 0,0931 à recopier vers la droite :

Après 3 itérations on a : 0,939 < x₀ < 0,940.

cos() ≈ 0,939 à 10⁻³ près.

Télécharger la feuille de calcul balayage.xls

Avec la calculatrice TI-92 taper la fonction dans le menu ¨y=,
dans ¨TblSet régler l'origine à 0 et le pas à 0.1,
¨Table permet de vérifier dans le tableau de valeurs l'encadrement 0,9< x₀ < 1.

Recommencer avec l'origine en 0.9 et un pas de 0.01 et ainsi de suite.

5. Parties proportionnelles

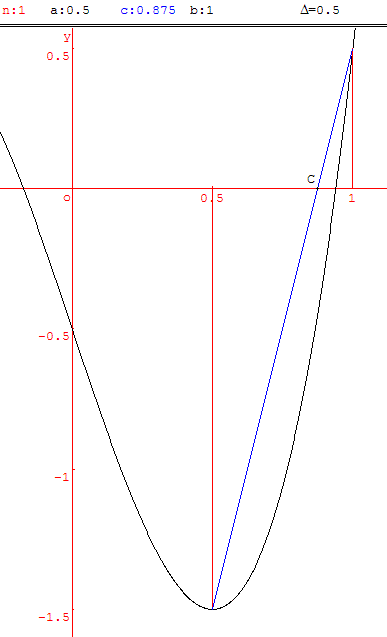
Supposons toujours que f(a) < 0 et f(b) > 0, et considérons la corde [AB] joignant les points A(a, f(a)) et B(b, f(b)).

D'après la figure, le point C d'intersection de cette corde avec l'axe des abscisses est déterminé par :

(c−a)/−f(a) = (b−c)/f(b)

soit c = (a f(b) − b f(a))/(f(b) − f(a))

Si nous remplaçons l'instruction de dicothomie :

(a+b)/2 → c

par l'instruction :

(a f(b)−b f(a))/(f(b)−f(a)) → c

on obtient la méthode des parties proportionnelles dont la convergence est, en général, un peu plus rapide que la dicothomie.

Après 4 itérations on a cos() ≈ 0,939 7 à 10⁻⁴ près.

Télécharger la figure GéoPlan trisec_propor.g2w

6. Point fixe

De l'équation 4 x³ − 3x − = 0 on trouve 4 x³ = 3x + et x = (3x + )^1/3 permet de trouver une suite x_n+1 = (3 x_n + )^1/3.

Avec x₁ = 1 on calcule en 3 itérations x₄ = 0,940 à 10⁻³ près ; x₁₃ = 0,939 692 6 à 10⁻⁷ près ;
et x₂₁ = 0,939 692 620 786 donne sur la TI-92 les 12 décimales de cos() en 20 itérations.

Méthode de Newton

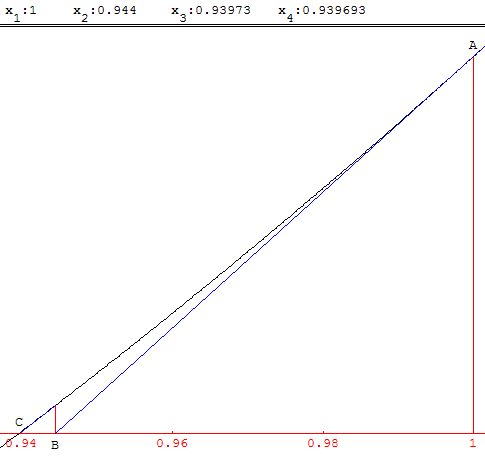
a est une valeur approchée de la solution cherchée. On détermine le point B d'intersection de l'axe des abscisses avec la tangente au point A(a, f(a)) à la courbe représentative de f.

La tangente en A a pour équation y − f(a) = f’(a)(x − a).
Elle coupe l'axe au point B tel que f(a) = f’(a)(x − a),
il résulte x = a − f(a)/ f’(a).

La fonction itérative de Newton g(x) = x − f(x)/ f’(x) permet de trouver une suite
x_n+1 = g(x_n) = x_n − f(x_n)/ f’(x_n) qui converge très rapidement vers la solution.

Ici g(x) = (16x³ + 1) /(6(2x +1)(2x − 1)).

Avec x₁ = 1 on calcule au moins deux décimales à chaque itération :
x₂ = 0,944 ; x₃ = 0,939 725; x₄ = 0,939 692 241

et enfin x₅ = 0,939 692 620 786 donne sur la TI-92
les 12 décimales de cos() en 4 itérations.

Avec la calculatrice TI-92, choisir l'option suite dans le menu mode, puis taper la suite u1(n) en fonction de u1(n−1) dans le menu ¨y= avec ui1 = 1.

Préparer la construction de «l'escargot » en choisissant dans menu F7 Axes de cet écran le mode TOILE d'araignée WEB.

La courbe et la droite d'équation y = x apparaît dans l'écran ¨Graph, choisir le mode F3 TRACE et afficher « l'escargot » en répétant l'appui sur la « flèche suivante ».

Remarque : la courbure étant très faible, la courbe et la tangente sont peu différenciées, et sur le petit écran de la calculatrice «l'escargot » est difficilement visible.

Télécharger la figure GéoPlan trisec_newton.g2w

7. Fractions continues

Comme cos() est compris entre et 1 le premier terme de la fraction continue est 1 et on substitue à x la fraction 1/(1+1/y) dans l'équation (E).
On obtient une équation admettant une solution positive comprise entre 15 et 16 ce qui permet de trouver cos() = [0, 1, 15…].

1/(1+1/15) < cos() < 1/(1+1/16) soit 15/16 < cos() < 16/17

Avec la calculatrice TI-92, la substitution 4 x^3 − 3 x − 1/2 | x = 1/(1+1/y) renvoie
1/2 − (9y² +6y+1)/(y+1)³.

Factoriser pour obtenir (y³−15y³−9y−1)/(2 /(y+1)³).

Effacer le dénominateur ou utiliser la fonction numér(.

Et résoudre l'équation y³ − 15y³ − 9y − 1 = 0.

Termes suivants

Dans y³−15y³−9y−1 substituer y = 15+1/z. L'équation −136z³ + 216z² + 30z + 1 admet une solution comprise entre 1 et 2. On a donc un quatrième terme égal à 1.

cos() = [0, 1, 15, 1…]

1/(1+1/(15+1/2)) < cos() < 1/(1+1/(15+1/1)) soit 31/33 < cos() < 16/17

Continuer en substituant z = 1 + 1/t, et ainsi de suite…

8. Développement de cos(2x)

Nous allons chercher un algorithme pour calculer une suite convergeant vers cos(x).

cos(2x) = cos²(x) − sin²(x) = 1 − 2sin²(x).

Pour x petit sin(x) ≈ x ; cos(x) = 1 − 2sin²() ≈ 1− x²/2.

Posons C(x) = 1 − cos(x) ≈ x²/2, on a C(2x) = 2C(x)(2 − C(x)).

Si on se donne la valeur approchée de C(x/2ⁿ) comme valeur initiale : x²/(2 × 4ⁿ) → C,
et en utilisant n fois l'instruction 2C(2−C) → C, on obtient C(2ⁿ (x/2ⁿ)) = C(x) et 1 − C(x) est une valeur approchée de cos(x).

Calculatrices TI-92, Voyage 200

Rédiger l'algorithme dans l'éditeur de programmes :

kos(x)
Prgm
18 → n
x^2/(2*4^n) → c
For i,1,n
  2*c*(2−c) → c 
EndFor
Disp 1−c
EndPrgm

Puis exécuter le programme, après avoir choisi le mode approché, en tapant dans la fenêtre ¨Home : kos(π/9)
pour obtenir 12 décimales de cos().

Capes, page n^o 3, créée le 18/4/2007