Abul-Wafa
Abu'l-Wafa (Abu l-Wafa ou Abul Wafa) est un mathématicien et astronome persan connu pour ses apports en trigonométrie et pour ses constructions à la règle et au compas.
Il est né en 940 à Buzjan dans la région de Khorasan. À l'âge de vingt ans, il part pour Bagdad où il restera jusqu'à sa mort en 998.
Il s'est particulièrement intéressé aux problèmes « d'inscription » ou de « circonscription » (pour construire des fresques comme dans l'Alhambra de Grenade) ce qui l'a conduit à écrire un ouvrage intitulé « Livre sur ce qui est nécessaire à l'artisan en science de la géométrie ».
Voir : problème d'Abul-Wafa - triangle équilatéral inscrit dans un carré
Tangram d'Abul Wafa - faire pivoter de deux triangles rectangles découpés au-dessus de la droite des milieux
Carré d'aire trois fois plus grande
Astronome et mathématicien grec 262/190 avant J.-C.
C'est à Apollonius que l'on doit les appellations des sections planes du cône : parabole, ellipse et hyperbole.
Théorème d'Apollonius : formule du théorème de la médiane,
Cercle tangent aux cercles exinscrits d'un triangle et point d'Apollonius,
Faisceau de cercles d'Apollonius dans un triangle,
Apollonius Gallus : problème des trois cercles,
Un problème d'Apollonius : cercle tangent à trois cercles.
Archimède (287-212 avant J.-C.)
Arbelos d'Archimède
Cercles jumeaux d'Archimède
Duplication du cercle
Parabole : quadrature d'Archimède
Ellipse : construction d'Archimède
Trisection : méthode d'Archimède
Heptagone
Les trois hauteurs d'un triangle sont concourantes au même point.
Solide d'Archimède : Polyèdre semi-régulier dont les faces sont des polygones réguliers, ceux-ci pouvant être différents, mais disposés dans le même ordre autour de chaque sommet.
Tétraèdre tronqué
Conoïdes
Babylone
Calcul approché de 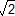
Puzzle de Pythagore
Brahmagupta (mathématicien indien du VIIe siècle)
Théorème de Brahmagupta :
si les diagonales d'un quadrilatère inscriptible sont perpendiculaires l'une à l'autre et se coupent en un point O, une droite passant par O et perpendiculaire à l'un quelconque des côtés coupe le côté opposé en son milieu.
Brocard
Catalan : mathématicien belge, 1814-1894
L'hexagone ayant pour sommets les projections des pieds des hauteurs sur les deux autres côtés d'un triangle est l'hexagone de Catalan.
Céva Giovanni : mathématicien italien 1648-1734
Théorème de Céva
Théodore de Cyrène
Spirale
Desargues
Girard Desargues (Lyonnais 1591-1661) est le créateur de la géométrie projective, étude de propriétés qui se conservent par projection centrale : alignement, point de concours et birapport.
René Descartes, généralement connu pour son œuvre philosophique, fut aussi un grand mathématicien.
Son apport principal dans ce domaine est la numérisation de la géométrie.
La Géométrie
Professeur de l'ancien lycée René Descartes de Bouaké, je voulais présenter l'œuvre mathématique de cet auteur.
Je propose donc le texte et des commentaires de la géométrie à propos du théorème de Thalès, des problèmes du second ou du troisième degré.
Voir aussi, dans le problème de Pappus, les coniques comme lieux de points (niveau bac + 2).
Le café pédagogique : Il y a quelques années, nous vous avions recommandé le site de P. Debart. Depuis, il a bien évolué : nous vous incitons à aller explorer le travail relatif à Descartes. La lecture des textes mathématiques du célèbre philosophe y est accompagnée de figures interactives du meilleur effet.
Il donne une méthode pour déterminer la normale à certaines courbes.
Pour cela, il cherche le centre du cercle osculateur touchant la courbe selon un point double. Ce cercle est tangent à la courbe et son centre placé sur la perpendiculaire à la tangente.
Il procède ainsi pour la conchoïde de Nicomède.
Il utilise également cette méthode pour ses ovales, en rapport avec la fabrication de lentilles optiques de qualité.
Il détermine également quelle est la tangente en un point de la cycloïde.
Relation de Descartes
Quatre points distincts alignés A, B, C, D sont en division harmonique si, et seulement si, on a la relation : 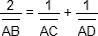 . .
Théorème de Descartes
Ce théorème, découvert par René Descartes en 1643, établit une relation entre les rayons de quatre cercles tangents entre eux.
Il peut être utilisé pour construire un quatrième cercle tangent à trois autres.
Dürer
« Albert Dürer (né à Nuremberg en 1471, mort en 1528) appartient, comme Léonard de Vinci, à cette génération de grands artistes, peintres, sculpteurs et architectes, pour lesquels la géométrie est non seulement un instrument d'analyse, mais un puissant moyen de perfectionnement.
L'étude de la perspective le conduisit à la transformation des figures en d'autres figures du même genre. Et de là naquirent plusieurs méthodes géométriques,
comme celle qui consiste à faire croître proportionnellement les ordonnées des points d'une figure, dans le dessin d'un profil dont on veut rendre les dimensions en hauteur plus facilement appréciables.
Dürer maniait très habilement le compas pour tracer des ellipses et d'autres figures géométriques.
Le pentagone de Dürer est un pentagone, construit avec une seule ouverture de compas ; mais d'autres géomètres ont démontré depuis que ce pentagone n'a pas tous les angles égaux et que sa figure n'est qu'approximative. »
(Alexandrie, 300 avant Jésus-Christ)
Les treize livres des Éléments d'Euclide constituent une synthèse remarquable des mathématiques grecques.
Ils ont fondé la méthode synthétique qui, à partir des propriétés géométriques établies précédemment, permet de déduire la propriété cherchée.
Toutes les constructions s'y effectuent uniquement à la règle et au compas.
Euler (1707-1783)
Cercle et droite d'Euler
Ellipse d'Euler
Centre d'Euler d'un quadrilatère.
En 1767, Euler publia une des premières étude sur les centres d'un triangle.
Méthode de résolution numérique d'une équation différentielle où on remplace la dérivée par l'approximation au premier ordre obtenue à partir d'une valeur de la fonction et de celle au pas de temps suivant.
Quatre relations d'Euler
Dans l'espace
Relation entre le nombre de faces, de sommets et d'arêtes d'un polyèdre convexe.
La formule d'Euler la plus célèbre concerne les polyèdres convexes : f + s = a + 2 où f est le nombre de faces, s le nombre de sommets et a le nombre d'arêtes.
C'est Euler qui démontrera cette formule, énoncée par Descartes.
Dans le triangle
Si O est le centre du cercle circonscrit et H l'orthocentre d'un triangle ABC, alors 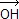 = = 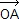 + + 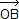 + + 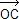 . .
Si O est le centre du cercle circonscrit d'un triangle, H l'orthocentre et G le centre de gravité, les points O, G et H sont alignés sur une droite dite droite d'Euler.
GH = 2 GO (relation d'Euler : G est au tiers de [OH] ).
Distance entre les centres des cercles inscrit et circonscrit
Si le cercle circonscrit d'un triangle a pour centre O et pour rayon R et le cercle inscrit a pour centre I et pour rayon r, la relation d'Euler permet de calculer le carré de la distance des deux centres :
OI2 = R2 - 2Rr.
Démonstration : voir la puissance du point I par rapport au cercle circonscrit (c) et un cercle (Γ).
Fagnano (mathématicien italien 1682-1766)
Problème de Fagnano : dans un triangle, trouver un triangle inscrit de périmètre minimum.
Feuerbach (1800-1834)
Théorème : dans un triangle, le cercle d'Euler est tangent au cercle inscrit et aux trois cercles exinscrits.
Le point de contact entre le cercle d'Euler et le cercle inscrit s'appelle le point de Feuerbach.
Théorème découvert en 1822 par Feuerbach, puis démontré par M'Clelland en 1891 et Lachlan en 1893.
Léonard de Pise dit Fibonacci (1170-1250)
Son œuvre fondamentale fut l'introduction des chiffres indo-arabes, du zéro et la notation positionnelle du système décimal.
Suites et Fibonacci, nombre d'or
Une histoire couple de lapins qui donnent naissance à un couple d'animaux qui à la génération suivante donne naissance à un nouveau couple et ainsi de suite… (livre de l'abaque «Liber Abaci» paru en 1202).
Les « anciens Égyptiens » ne connaissaient, comme fractions, que les inverses de naturels de numérateur 1.
Ils écrivaient les rationnels de ] 0 ; 1 [ comme sommes d'inverses de naturels strictement croissants.
Gauss
Théorème de Gauss
Heptadécagone (polygone de Gauss) : la construction employée par Gauss en 1796, fut simplifiée par William Richmond en 1893.
Gergonne Joseph (mathématicien français 1771-1859)
Théorème de Gergonne (Coordonnées barycentriques d'un point dans un plan)
Point et triangle de Gergonne (Points de contact des côtés d'un triangle avec le cercle inscrit)
Points et nombres constructibles
Quadrature du cercle : π et le papyrus Rhind
Duplication du carré et du cube
Trisection de l'angle : la quadratrice de Dinostrate
Héron d'Alexandrie (Ier siècle)
relations métriques du triangle
Calcul approché de 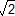
Hippocrate de Chios vers 450 avant J.-C. (- 470 ?, - 410 ?)
ABC étant un triangle rectangle en C, les lunules d'Hippocrate sont les deux croissants compris entre les demi-cercles de diamètres [AC] et [CB] (construits extérieurement au triangle) et les arcs AC et CB du demi-cercle de diamètre [AB] circonscrit au triangle.
Au Ve siècle avant J.-C., Hippocrate de Chios prouva la « quadrature » des lunules : l'aire du triangle rectangle est égale à la somme des aires de deux lunules.
Hyperbole de Descartes
Félix Klein (1849-1925)
Programme d'Erlangen : problèmes célèbres de la géométrie élémentaire
Transformer un quadrilatère en triangle
La quadrature du rectangle
Trisection d'un angle droit
FAMOUS PROBLEMS OF ELEMENTARY GEOMETRY
Gottingen, Easter, 1895.
1. The problem of the duplication of the cube (also called the Delian problem).
2. The trisection of an arbitrary angle.
3. The quadrature of the circle, i.e., the construction of pi.
The Division of the Circle into 15 Equal Parts.
The Construction of the Regular Polygon of 17 Sides.
Lambert Jean-Henri (1728-1777)
Les 15 problèmes de géométrie de la règle
Sébastien Leclerc (1637-1714)
Traité de géométrie théorique et pratique à l'usage des artistes - 1674
Mathématicien français, spécialiste de la géométrie du triangle, 1840 - 1912.
Les trois symédianes d'un triangle sont concourantes. Leur point de concours est le point de Lemoine ou point symédian du triangle.
Liu Hui
Chine, époque Han, IIIe siècle
Preuves du théorème de Pythagore : puzzle de Gougu,
puzzle de Bhaskara
Lucas Édouard (mathématicien français, 1842-1891)
Lucas systématisa les suites définies par la double récurrence un+2 = un + un+1,
Il a nommé la suite 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… suite de Fibonacci et nombres de Fibonacci les termes de cette suite.
La suite de Lucas a pour conditions initiales u0 = 2 et u1 = 1.
Voir aussi : construction du pentagone par nœud d'une bande
Marolois Samuel
La quadrature du rectangle (1617)
Construction du carré à partir d'un côté
Mathématicien grec de la fin du Ier siècle, auteur de trois livres,dont les sphériques consacrées aux triangles sur une sphère.
Miquel (Théorèmes de Miquel)
Quadrilatère complet, point de Miquel et points cocycliques : plan projectif
Autres concours de cercle, démontrés par Miquel, voir : triangles de Napoléon
Théorème des cinq cercles : cercles en seconde
Nagel
Napoléon
Triangles de Napoléon : constructions avec des triangles équilatéraux
Triangles attribués à l'empereur. D'après Henri Lebesgue, Lagrange lui aurait dit : « Mon
Général, nous nous attendions à tout de vous, sauf à des leçons de géométrie ».
Problème de Napoléon, retrouver le centre d'un cercle au compas seul.
Isaac Newton est un philosophe, mathématicien, physicien et astronome et théologien anglais, né le 4 janvier 1643. décédé le 31 maes 1727.
Théorème de Newton dans un quadrilatère complet : les milieux des diagonales sont alignés sur une droite appelée droite de Newton du quadrilatère.
Droite de Newton d'un triangle.
Relation de Newton pour une division harmonique : [A, B, C, D] = −1 si et seulement si IA2 = IB2 = 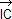 . . 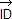 où I est le milieu de [AB]. où I est le milieu de [AB].
Trident de Newton (ou parabole de Descartes)
Nicomède
Mathématicien grec du IIe siècle avant J.-C., avec la conchoïde, il fut le premier à réaliser une construction mécanique d'une courbe plane (autre que le cercle).
Œnopide de Chios (Ve siècle avant J.-C.) : construction de lamédiatrice
Eudème, cité par Proclus, attribuait à Œnopide de Chios (Ve siècle avant J.-C.),
la découverte du problème relatif à la proposition 23 du livre I d'Euclide : « Sur une droite donnée,
et en un point donné sur cette droite, construire un angle égal à un angle donné. »
La parabole chez les Anciens
Pappus d'Alexandrie
Pappus est l'un des plus importants mathématiciens de la Grèce antique. Il est né à Alexandrie et a vécu au IVe siècle.
Théorème de Pappus : plan projectif
Petit théorème de Pappus
Parallélogramme de Pappus : preuve par homothétie
Démonstration par Pappus du théorème de Pythagore
Problème de Pappus
Étant donné quatre droites, le problème est la recherche du lieu géométrique des points dont les segments menés de ce point à chacune des droites suivant des directions données ont des produits égaux.
Le problème de Pappus a permis à Descartes d'expliciter, dans sa géométrie, ses théories sur « la nature des courbes planes ».
Note sur le problème de Pappus
Autres problèmes de Pappus
– échelle contre un mur
– cercles tangents en chaîne
Voir Pappus d'Alexandrie
Platon (428 à 348 avant J.-C.)
Duplication du carré
Solides de Platon,
Platon affirmait que toute la connaissance réside dans le nombre d'or.
Poncelet Mathématicien français (1788-1867)
Ptolémée (milieu du IIe siècle) : pentagone, quadrilatère inscriptible
Inventeur de la cartographie.
Pythagore : démonstrations géométriques du théorème
Sierpinski
Socrate
Duplication du carré
Sulbasutras
Construction du carré à partir d'une médiatrice
Constructions de carrés d'aire égale à la somme ou la différence des aires de deux carrés rel="nofollow"
La quadrature du rectangle
Taylor
Terquem
Thalès
théorème de Thalès : GéoPlan
polygone : construction dite « de Thalès »
Thébault Victor 1882-1960
Théorème de Thébault :
quatre carrés à l'extérieur d'un parallélogramme
deux triangles équilatéraux autour d'un carré
le théorème de Thébault − Sawayama
Evangelista Torricelli (1608-1647)
parabole
Tücker
Variable x
La lettre x est généralement utilisée pour désigner une inconnue ou une variable.
Pour Al-Khwârizmî (mathématicien persan, vers 780-858) l'inconnue est « la chose ».
Le mot persan est devenu chay en arabe et a été transcrit en xay en espagnol.
Al-Qalasadi (mathématicien andalou, 1412-1486) utilisait alors la première lettre de xay en notant l'inconnue x,
Descartes a systématisé l'utilisation des lettres de la fin de l'alphabet x, y, z pour les variables.
Pierre Varignon (1654-1722), ami de Jean Bernouilli, est surtout connu pour avoir assis en France les idées de Leibniz
sur l'analyse (reprises par De L'Hospital) face à l'opposition de Rolle et aux travaux de Newton.
Wantzel Pierre-Laurent
Mathématicien français, a montré en 1837 qu'un nombre constructible est algébrique sur Q et son degré est une puissance de 2.
La réciproque est très utile pour montrer qu'un nombre n'est pas constructible.
Viète
Apollonius Gallus : problème des trois cercles
Méthode de Viète ou des translations parallèles :
Cercles tangents, tangents aux côtés d'un triangle
Deux cercles tangents, tangents à l'intérieur d'un cercle
Trisection, 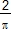 : Formule de Viète : Formule de Viète
Léonard de Vinci
Duplication du carré
Wallis
Construction d'une moyenne géométrique
Application à :
la quadrature du rectangle
calcul d'une racine carrée
|  Descartes et les Mathématiques
Descartes et les Mathématiques![]() Sur tablette numérique ou smartphone, bascule automatique vers la version mobile
Sur tablette numérique ou smartphone, bascule automatique vers la version mobile![]() sur une tablette babylonienne
sur une tablette babylonienne![]() , π : petits programmes
, π : petits programmes