Terminale ES

2.1. Droites et plans dans l'espace
Bac ES national 1999 - spécialité
2.2. Plan et droite dans un pavé
Bac ES Amérique du Nord 1999

1.1. Perdu dans l'espace

geometrie dans l'espace - cube perdu dans l'espace - copyright Patrice Debart 2007

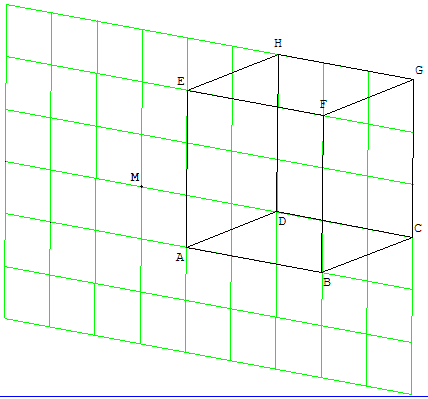
Les ambiguïtés de la perspective cavalière

On représente en perspective cavalière un cube ABCDEFGH et un point M selon la figure ci-contre.
Le point M est-il à gauche ou sur la droite du cube ci-contre ?

Indications

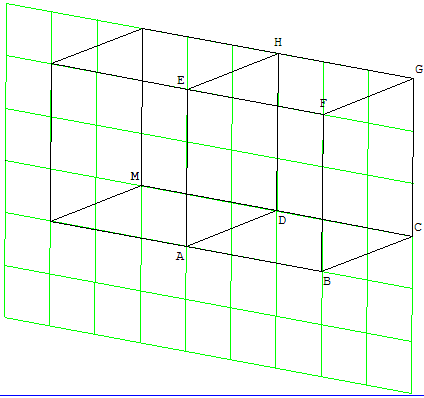
Comme dans la figure ci-dessous le point M peut représenter un point situé sur la droite (CD), à gauche.

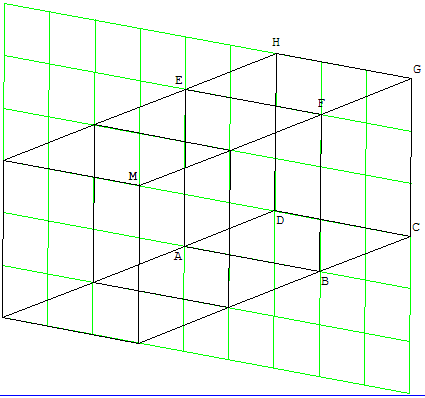
Mais en dessinant deux cubes devant le cube initial, la figure en bas à droite montre que M peut représenter un point de la droite (GF), sur le côté droit du cube !

Si M₁ est le point de l'espace situé sur (CD) et M₂ est le point de l'espace situé sur (GF), le point M peut représenter n'importe quel point de la droite (M₁M₂).

Télécharger la figure GéoSpace perdu_espace.g3w

Voir : activités

geometrie dans l'espace - 2 cubes perdus dans l'espace - copyright Patrice Debart 2007

geometrie dans l'espace - 3 cubes perdus dans l'espace - copyright Patrice Debart 2007

1.2. Solides définis par leurs équations

Exemples d'exercices pour l'articulation « première terminale » en série S

Dans l'espace muni d'un repère orthonormal.

Déterminer les solides définis par les équations suivantes :

a) x² + y² + z² = 4

b) x² + y² = 4

Voir : quadriques et GéoSpace

1.3. Distribuer une section plane déjà construite

Demander aux élèves de tracer les points « hors solide » qui ont permis d'obtenir cette section. Autrement dit, leur faire faire des exercices sur les sections dans les deux sens.

1.3.a. Section d'un cube par le plan (PQR)

geometrie dans l'espace - section plane de cube - copyright Patrice Debart 2007

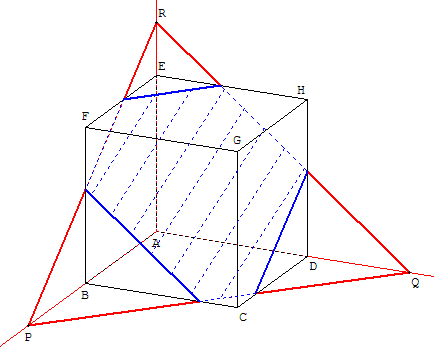
À partir du plan (PQR), trouver la section plane.

Dans l'autre sens, à partir de la section plane, retrouver les points P, Q et R situés sur les prolongements des côtés.

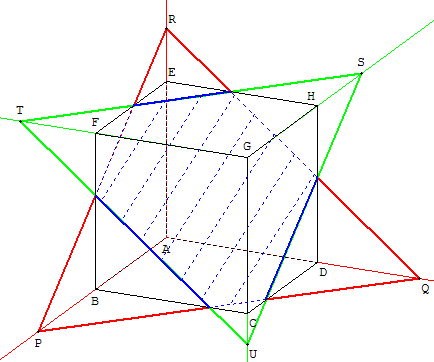
On peut ensuite trouver les points S, T et U situés sur les prolongements des trois autres côtés.

Télécharger la figure GéoSpace section_cube.g3w

Commandes GéoSpace

Touche 1 : afficher /effacer le plan (PQR)
Touche 2 : afficher /effacer le plan (STU)
Touche 3: afficher /effacer la section plane

1.3.b. Section plane triangulaire d'un cube

geometrie dans l'espace - section triangulaire de cube - copyright Patrice Debart 2007

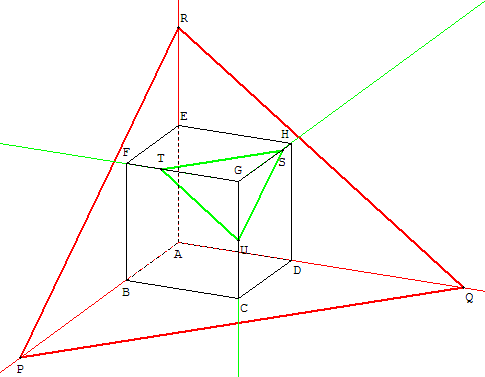
Moins facile.

À partir du plan (PQR), trouver la section plane STU.

Dans l'autre sens, à partir de la section plane STU, retrouver les points P, Q et R situés sur les prolongements des côtés.

Voir correction dans avec GeoGebra 3D en première

Télécharger la figure GéoSpace section_cube2.g3w

Figure 3D dans GeoGebraTube : prolongement d'une section triangulaire du cube

Terminale ES

2.1. Droites et plans dans l'espace

Bac ES national 1999 :
Exercice II Géométrie (spécialité en mathématiques)

bac S maths 1999 - geometrie analytique dans l'espace - droites et plans - copyright Patrice Debart 2007

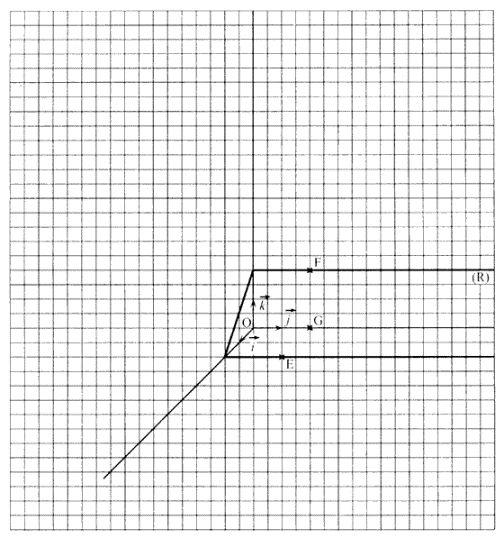
L'espace est muni d'un repère orthonormal (O, , , ) représenté ci-après.
Le plan (R) est représenté par ses traces sur les plans de coordonnées ; il a pour équation : x + z = 2.

On donne les points A, B, C, définis par leurs coordonnées respectives : A(6 ; 0 ; 0) B(0 ; 3 ; 0) et C(0 ; 0 ; 6)

2.1.a. Placer les points A, B, C dans le repère (O, , , ) et tracer le triangle ABC.
2.1.b. Calculer les coordonnées des vecteurs et .

2.1.c. Soit le vecteur de coordonnées (1 ; 2 ; 1).
Montrer que le vecteur est normal au plan (P) passant par A, B et C.

Vérifier que le plan (P) a pour équation x + 2y + z = 6.
On a placé dans le repère les points G, E, et F à coordonnées entières.

Le point G est situé sur l'axe (O,), le point E dans le plan (O, , ) et le point F dans le plan (O, , ).
Le plan (Q) passant par les points G, E, et F est parallèle au plan (O, , ) ;

a. Donner l'équation du plan (Q).
b. Donner les coordonnées des points G, E et F.
c. Parmi les points E, F et G quels sont ceux situés sur le plan (P) ?

d. Quelle est la nature de l'ensemble des points M dont les coordonnées (x ; y ; z) vérifient le système :

Représenter cet ensemble sur la figure ci-dessous.
On considère le système S de trois équations à trois inconnues x, y, z :

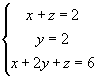
Quel est l'ensemble des points du plan dont les coordonnées sont solutions du système S ?

2.2. Plan et droite dans un pavé

Bac ES Amérique du Nord 1999

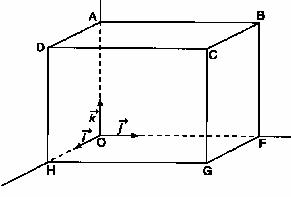
L'espace est rapporté au repère orthonormal (O ; , , ).
ABCDOFGH est un pavé défini par OH = 3, 0F = 4 et OA = 3 .
Soit L le milieu de [CG].

bac es maths 1999 - géométrie analytique dans l'espace - pavé droit - copyright Patrice Debart 2007

1. On considère l'ensemble P des points dont les coordonnées x, y et z vérifient :
4x - 3y + 8z - 12 = 0.
a. Parmi les points A, B, O, G, H, L lesquels appartiennent à P ?
b. Justifier que l'ensemble P est le plan (BLH).

2. a. Donner les coordonnées d'un vecteur normal au plan (BLH).
b. Soit D la droite passant par A et de vecteur directeur .
Montrer que D est l'ensemble des points M tels que 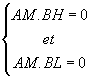AM.BH=0 et AM.BL=0
En déduire un système d'équations caractérisant la droite D.

c. Montrer que le point de coordonnées appartient à D et à P.

Indications

Les coefficients de l'équation de P permettent de trouver les coordonnées : (4, -3, 8).

orthogonal au plan P, est orthogonal aux deux vecteurs et non colinéaires contenus dans ce plan.
M appartient à la droite D si et seulement si est orthogonal à et , dons si les produits scalaires . et . sont nuls.
(x, y, z-3) (3, -4, -3) ; . = 0 conduit à l'équation 3x - 4y - 3(z-3) = 0.
(3, 0, -) ; . = 0 conduit, après simplification, à l'équation 2x - (z-3) = 0.

Le système formé par ces deux équations 3x - 4y - 3z + 9 = 0 et 2x - z + 3 = 0 caractérise la droite D, intersection des deux plans correspondant à ces deux équations.

Télécharger la figure GéoSpace pave_droite_plan.g3w