Descartes et les Mathématiques
Sections planes d'un cube
La géométrie dans l'espace dans l'ancienne 1ère S
Sur tablette ou smartphone, cette page lance automatiquement la version GeoGebra 3D
Triangle, quadrilatère, pentagone et hexagone comme sections planes d'un cube.
Intersection d'un plan avec les faces du cube
2. Constructions de sections par des plans variables
3. Variation de la section par un plan variable
4. Un sommet et deux points sur les arêtes
5.a. Trois points sur des arêtes concourantes
5.b. Trois points sur des arêtes non concourantes
6. Trois points sur des arêtes disjointes
Sections planes du cube dans d'autres pages du site
Plan et droite orthogonaux dans le cube, à l'épreuve pratique de TS
Problème de Bergson à l'épreuve pratique de TS
Section d'un cube par un déterminé par trois points situés sur le cube
Sections planes : avec GéoSpace il est facile de créer la section d'un cube par un plan passant par trois points.
Lorsque l'on s'intéresse uniquement au résultat, il est possible de créer facilement la section, par le plan passant par les trois points, avec le menu
Ligne>Polygone convexe>Section d'un polyèdre par un plan.
Dans ce cas, les sommets de la section ne sont pas nommés, donc non réutilisables.
Géométrie pratique
- Une solution non conformiste, piochée de-ci, de-là dans l'exercice 497-3 de l'APM, consiste à marquer les trois points sur un cube et de le plonger délicatement dans un bain de teinture colorée.
En retirant le cube, la section apparaît. - Une autre solution consiste à remplir d'eau un bidon en plexiglas transparent que l'on a percé à l'emplacement des trois points.
En inclinant le bidon, de telle façon que l'eau sorte par les trois trous, le niveau d'eau donne la section. - Une dernière solution consiste à traverser ce cube, en plexiglas transparent, par un balayage de rayons laser passant par les trois points.
En général, dans les exercices ci-dessous nous décrivons la construction point par point des sections, en explicitant les divers cas particuliers.
1. Sections d'un cube par un plan déterminé par trois points situés sur les arêtes
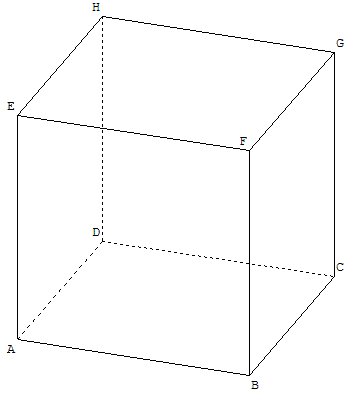
1.a. Ouvrir le fichier GéoSpace « cube.g3w ». ABCDEFGH est un cube.
Figures 3D dans GeoGebraTube : cube, cube en fil de fer
1.b. Créer les points variables M, N et P sur les arêtes respectives [FB], [FG] et [EF], concourantes au même sommet F.
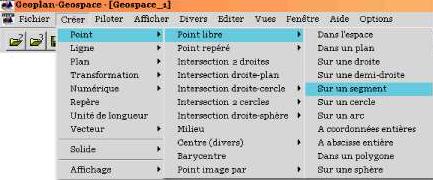
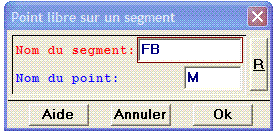
1.c. Créer la section du cube par le plan (MNP).
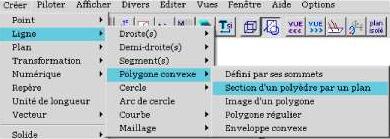
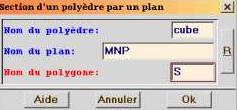
On pourra hachurer en couleur la section obtenue (utiliser la boîte de style 
).
Suite à la demande de Mathieu : Coupe d'un cube par un plan les membres du site bouge pour la planète ont soumis des ressources au vote.
Ci-contre voici la photo plébiscitée par la communauté bougepourtaplanete.fr en 2014 pour Coupe d'un cube par un plan
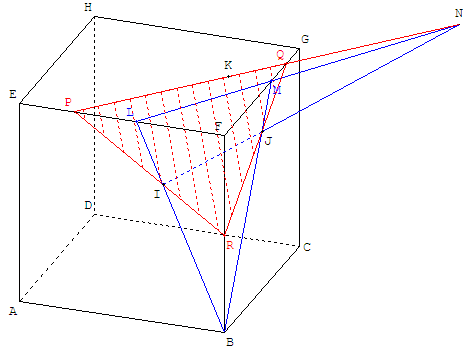
Plan déterminé par trois points sur trois arêtes concourantes
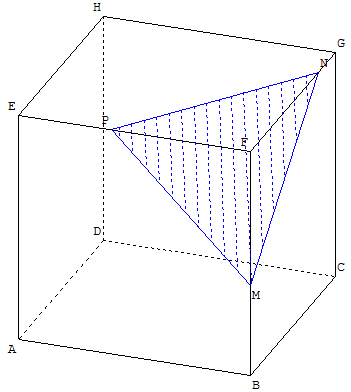
1.d. Déplacer (clic gauche sur la souris) les points M, N et P et observer la section obtenue.
Figure 3D dans GeoGebraTube : triangle comme section plane du cube
Retrouver cette figure :
Voir l'intersection du plan (MNP) avec les six faces du cube
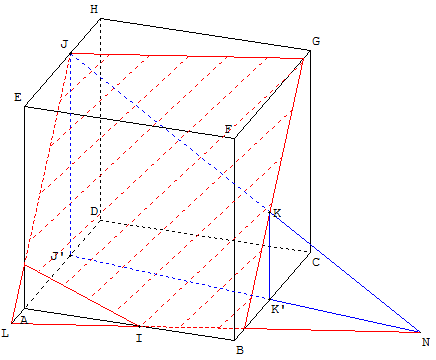
Deux points sur deux arêtes concourantes et un troisième
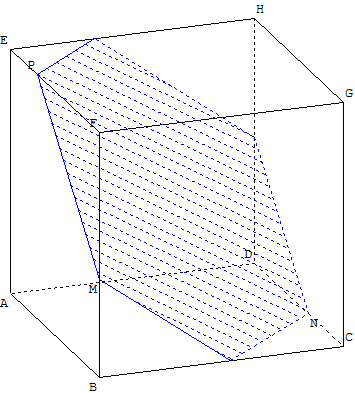
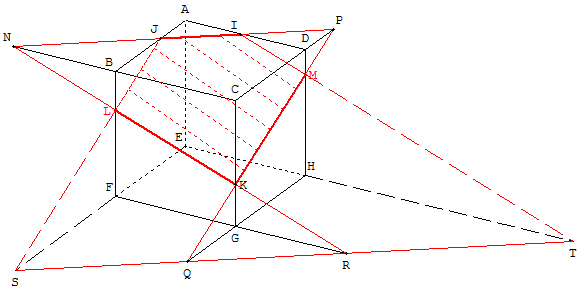
1.e. Modifier le point N pour qu'il se déplace maintenant sur l'arête [DC],
créer la section du cube par le plan (MNP),
déplacer les points M, N et P et observer les diverses sections obtenues :
si ces points ne sont pas des sommets du cube, on trouve des pentagones ou hexagones ayant deux ou trois paires de côtés parallèles.
Figure 3D dans GeoGebraTube : sections d'un cube déterminées par trois points
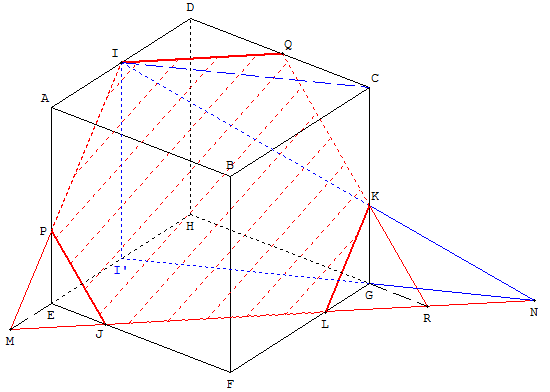
Trois points sur des arêtes disjointes dans les trois directions
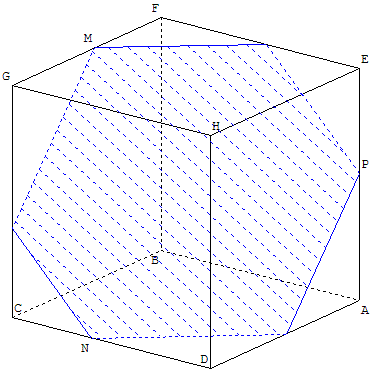
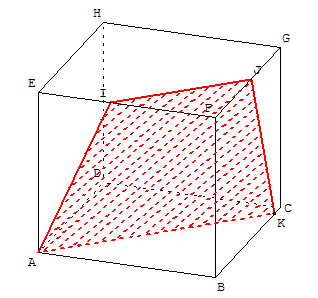
1.f. Modifier maintenant le point P pour qu'il se déplace sur l'arête [AE],
créer la section du cube par le plan (MNP),
déplacer les points M, N et P et observer les diverses sections obtenues:
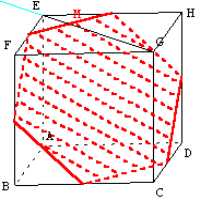
Si ces points ne sont pas des sommets du cube, on trouve des hexagones ayant des côtés deux à deux parallèles.
Lorsque M, N et P sont les milieux des côtés, on a l'hexagone régulier de Bergson.
Figure 3D dans GeoGebraTube : hexagone comme section d'un cube
2. Constructions de diverses sections par des plans parallèles
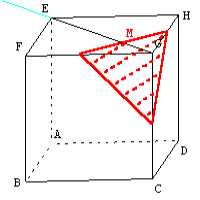
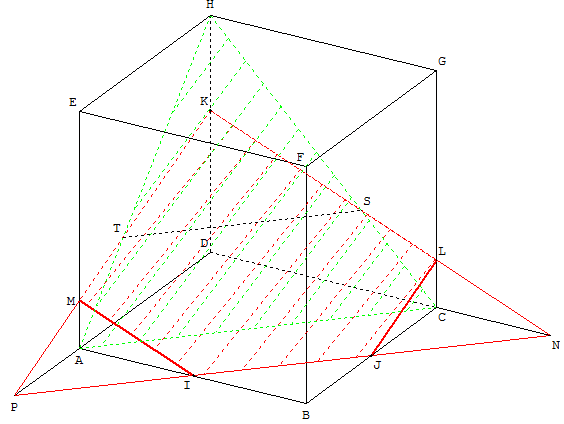
Triangle BMN et section par le plan parallèle passant par le sommet A
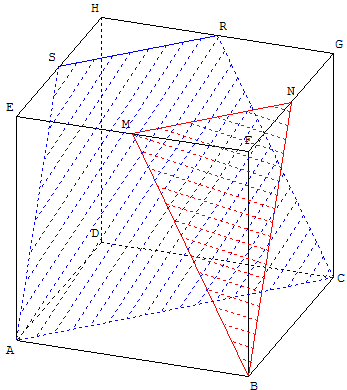
M est le milieu de [EF], N est le milieu de [FG].
Le triangle BMN est la section du cube avec le plan (BMN).
On mène par A le plan (P) parallèle au plan (BMN).
Construire la section du cube avec le plan (P).
Figures 3D dans GeoGebraTube : section d'un cube par un plan variable
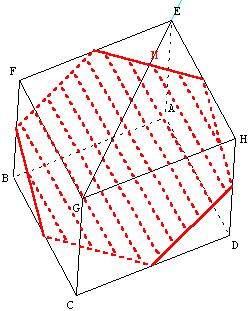
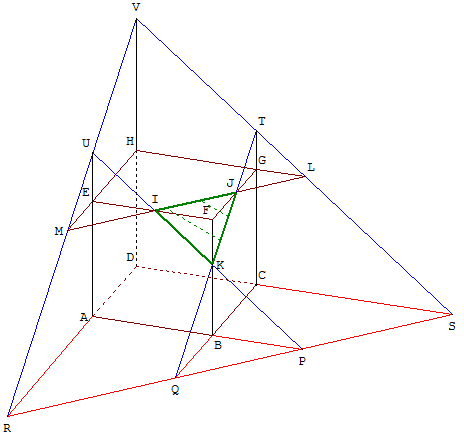
Triangle équilatéral BDE et section par un plan parallèle passant par un point M
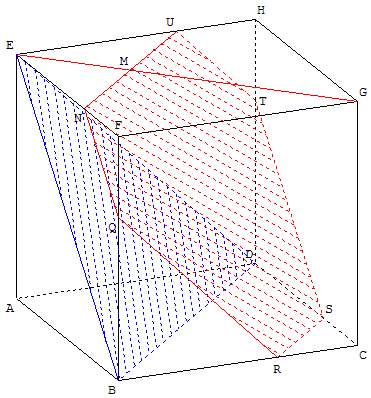
Construire le triangle BDE, section du cube avec le plan (BDE).
Soit M le point de la diagonale [EG],
tel que EM = 
EG.
Trouver l'intersection du cube avec le plan parallèle au plan (BDE) passant par M.
- Généralisation à un plan parallèle au plan (BDE) passant par un point M variable sur [EG],
Figures 3D dans GeoGebraTube : section d'un cube parallèle à trois diagonales
« L'utilisation de l'informatique permet une vision dynamique de la figure. GéoSpace permet de faire tourner le cube et de mettre en évidence la section cherchée. La possibilité de placer un plan isolé de face permet de voir les sections planes en “vraie grandeur”.
Les commandes “dessin en bloc” facilitent la présentation par le professeur avec un rétroprojecteur. »
a2.
